共找到2條詞條名為線性系統的結果 展開
- 數學模型種類
- 余貽鑫編著圖書
線性系統
數學模型種類
線性系統是一數學模型,是指用線性運運算元組成的系統。相較於非線性系統,線性系統的特性比較簡單。線性系統需滿足線性的特性,若線性系統還滿足非時變性(即系統的輸入信號若延遲τ秒,那麼得到的輸出除了這τ秒延時以外是完全相同的),則稱為線性時不變系統。
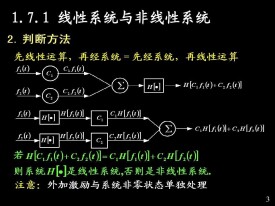
狀態變數(見狀態空間法)和輸出變數對於所有可能的輸入變數和初始狀態都滿足疊加原理的系統。疊加原理是指:如果系統相應於任意兩種輸入和初始狀態(u1,x01)和(u2(t),x02)時的狀態和輸出分別為(x1(t),y1(t))和(x2(t),y2(t)),則當輸入和初始狀態為(C1u1(t)+C2u2(t),C1x01+C2x02)時,系統的狀態和輸出必為(C1x1(t)+C2x2(t),C1y1(t)+C2y2(t)),其中x表示狀態,y表示輸入,u表示輸出,C1和C2為任意實數。一個由線性元部件所組成的系統必是線性系統。但是,相反的命題在某些情況下可能不成立。線性系統的狀態變數(或輸出變數)與輸入變數間的因果關係可用一組線性微分方程或差分方程來描述,這種方程稱為系統的數學模型。作為疊加性質的直接結果,線性系統的一個重要性質是系統的響應可以分解為兩個部分:零輸入響應和零狀態響應。前者指由非零初始狀態所引起的響應;後者則指由輸入引起的響應。兩者可分別計算。這一性質為線性系統的分析和研究帶來很大方便。
嚴格地說,實際的物理系統都不可能是線性系統。但是,通過近似處理和合理簡化,大量的物理系統都可在足夠準確的意義下和一定的範圍內視為線性系統進行分析。例如一個電子放大器,在小信號下就可以看作是一個線性放大器,只是在大範圍時才需要考慮其飽和特性即非線性特性。線性系統的理論比較完整,也便於應用,所以有時對非線性系統也近似地用線性系統來處理。例如在處理輸出軸上的摩擦力矩時,常將靜摩擦當作與速度成比例的粘性摩擦來處理,以便於得出一些可用來指導設計的結論。從這個意義上來說,線性系統是一類得到廣泛應用的系統。
線性系統是指同時滿足疊加性與均勻性(又稱為齊次性)的系統。所謂疊加性是指當幾個輸入信號共同作用於系統時,總的輸出等於每個輸入單獨作用時產生的輸出之和;均勻性是指當輸入信號增大若干倍時,輸出也相應增大同樣的倍數。對於線性連續控制系統,可以用線性的微分方程來表示。不滿足疊加性和均勻性的系統即為非線性系統。
由於線性系統較容易處理,許多時候會將系統理想化或簡化為線性系統。線性系統常應用在自動控制理論、信號處理及電信上。像無線通訊訊號在介質中的傳播就可以用線性系統來模擬。
線性
線性linear,指量與量之間按比例、成直線的關係,在數學上可以理解為一階導數為常數的函數;非線性non-linear則指不按比例、不成直線的關係,一階導數不為常數。
如問:兩個眼睛的視敏度是一個眼睛的幾倍?很容易想到的是兩倍,可實際是 6-10倍!這就是非線性。激光也是非線性的!天體運動存在混沌;電、光與聲波的振蕩,會突陷混沌;地磁場在400萬年間,方向突變16次,也是由於混沌。甚至人類自己,原來都是非線性的:與傳統的想法相反,健康人的腦電圖和心臟跳動並不是規則的,而是混沌的,混沌正是生命力的表現,混沌系統對外界的刺激反應,比非混沌系統快。
雙線性
式中分別是狀態向量和控制向量,上標T表示轉置;A,Pi和B均為常係數矩陣;dx/dt表示x對時間t的微商。這類狀態方程的特點是,它相對於狀態或控制在形式上分別是線性的,雙線性的名稱即源於此。但同時相對於狀態和控制來說,系統則不是線性的。它實際上是一類具有比較簡單形式的特殊非線性系統。雙線性系統模型是對線性系統模型的推廣,它能更準確地描述一類實際過程。生物繁殖過程就是一個典型的例子,用狀態變數x表示種群中生物體的數量,控制變數u表示可人為控制的凈增殖率,則控制種群中生物體數量的繁殖過程可用形式為dx/dt=ux的一個雙線性系統來描述。雙線性系統模型已被廣泛用於工程、生物、人體、經濟和社會問題的研究。例如,化學反應中的催化作用問題;人體內的水平衡過程、體溫調節過程、呼吸中氧和二氧化碳交換過程、心血管調節過程等問題;細胞內的某些生物化學反應問題;社會和經濟領域中的人口問題,動力資源問題,鋼鐵、煤炭、石油產品生產問題等。
雙線性系統的研究始於60年代,70年代以來得到了廣泛的重視和迅速的發展,成為非線性系統研究中比較成熟的分支之一。雙線性系統理論中已有的主要結果為:
① 雙線性系統具有變結構系統的一些特徵,因而有一定的自適應性(見適應控制系統)。
② 對於控制變數受限制(即控制變數的大小必須在一定的界限內)的情況,已經找到用頻率域語言表達的穩定性條件。
③ 雙線性系統具有比線性系統更好的能控性。即使控制變數受限制,系統仍可能是完全能控的。已經獲得系統完全能控的一些充分條件。
④ 用李雅普諾夫穩定性理論能夠求得雙線性系統的鎮定控制解,即可找到一個反饋控制律u=u(x)使系統實現全局穩定。這種控制函數是開關型或飽和型的,開關曲面(或曲線)對狀態變
而言是二次曲面(或曲線)。
⑤ 採用動態規劃或極大值原理已能解決雙線性系統的一些最優控制問題,如最速控制,最省燃料控制,以及離散雙線性系統和隨機雙線性系統的最優控制等。
雙線性系統理論已有不少實際應用的例子。例如核電站、核動力裝置中核裂變和熱交換過程的最優控制,人口預測和控制等。
疊加原理
狀態變數和輸出變數對於所有可能的輸入變數和初始狀態都滿足疊加原理的系統。疊加原理是指:如果系統相應於任意兩種輸入和初始狀態(u1(t),x01)和(u2(t),x02)時的狀態和輸出分別為(x1(t),y1(t))和(x2(t),y2(t)), 則當輸入和初始狀態為(C1u1(t)+C2u2(t),C1x01+C2x02)時,系統的狀態和輸出必為(C1x1(t)+C2x2(t),C1y1(t)+C2y2(t)),其中x表示狀態,y表示輸出,u表示輸入,C1和C2為任意實數。
一個由線性元部件所組成的系統必是線性系統。但是,相反的命題在某些情況下可能不成立。線性系統的狀態變數(或輸入變數)與輸出變數間的因果關係可用一組線性微分方程或差分方程來描述,這種方程稱為系統的數學模型。作為疊加性質的直接結果,線性系統的一個重要性質是系統的響應可以分解為兩個部分:零輸入響應和零狀態響應。前者指由非零初始狀態所引起的響應;後者則指由輸入引起的響應。兩者可分別計算。這一性質為線性系統的分析和研究帶來很大方便。
嚴格地說,實際的物理系統都不可能是線性系統。但是,通過近似處理和合理簡化,大量的物理系統都可在足夠準確的意義下和一定的範圍內視為線性系統進行分析。例如一個電子放大器,在小信號下就可以看作是一個線性放大器,只是在大範圍時才需要考慮其飽和特性即非線性特性。線性系統的理論比較完整,也便於應用,所以有時對非線性系統也近似地用線性系統來處理。例如在處理輸出軸上的摩擦力矩時,常將靜摩擦當作與速度成比例的粘性摩擦來處理,以便於得出一些可用來指導設計的結論。從這個意義上來說,線性系統是一類得到廣泛應用的系統。
對於線性系統,通常還可進一步分為線性時不變系統和線性時變系統。
線性時不變系統
線性時不變系統也稱為線性定常系統或線性常係數係數,其特點是,描述系統動態過程的線性微分方程或差分方程中,每個係數都不隨時間變化的常數。從實際的觀點而言,線性時不變系統也是實際系統的一種理想化模型,實質上是對實際系統經過近似化和工程化處理后所導出的一類理想化系統。但是,由於線性時不變系統在研究上的簡便性和基礎性,並且為數很多的實際系統都可以在一定範圍內足夠精確地用線性時不變系統來代表,因此自然地成為線性系統理論中的主要研究對象。
線性時變系統
線性時變系統也稱為線性變係數系統。其特點是,表徵系統動態過程的線性微分方程或差分方程中,至少包含一個參數為隨時間變化的函數。在現實世界中,由於系統外部和內部的原因,參數的變化是不可避免的,因此嚴格地說幾乎所有系統都屬於時變系統的範疇。但是,從研究的角度,只要參數隨時間的變化遠慢於系統狀態隨時間的變化,那麼就可將系統按時不變系統來研究,由此而導致的誤差完全可達到忽略不計的程度。
線性時不變系統和線性時變系統在系統描述上的這種區別,既決定了兩者在運動狀態特性上的實質性差別,也決定了兩者在分析和綜合方法的複雜程度上的重要差別。事實上,比之線性時不變系統,對線性時變系統的研究要遠為複雜得多,也遠為不成熟得多。

線性系統
1.設線性時不變系統狀態空間描述,引入坐標變換,則變換后系統的狀態空間可描述。
2.線性時不變系統引入坐標變換,其傳遞函數矩陣在線性非奇異變換下保持不變。對於線性時變系統,考察連續時間線性時變系統,狀態空間描述。
此時,系統在坐標變換即線性非奇異變換下的特性不同於時不變系統,時變系統的坐標變換中,變換矩陣一般取為時變矩陣並滿足可微性要求。
若引入坐標變換即非奇異變換x=P(t),P(t)為可逆且連續可微,則變換后的狀態空間描述。
其中,變換前和變換后的狀態空間中的係數矩陣。
線性系統理論是現代控制理論中最基本、最重要也最成熟的一個分支,是生產過程式控制制、信息處理、通信系統、網路系統等多方面的基礎理論。其大量的概念、方法、原理和結論對於系統和控制理論的許多學科分支,如最優控制、非線性控制、隨機控制、系統辨識、信號檢測與估計等都具有十分重要的作用。線性系統理論在1960年前後開始了從古典階段到現代階段的過渡,其重要標誌之一是卡爾曼(R.E.Kalman)系統的把狀態空間法引入到系統與控制理論中來。狀態空間法的基本特點是採用狀態空間這種內部描述取代傳遞函數那種外部輸入輸出描述,並對系統的分析和綜合直接在時間域內進行。狀態空間法可以同時適用於單輸入單輸出系統和多輸入多輸出系統,線性定常系統和時變系統。在此種方法中,用以表徵系統動力學特性的數學模型是反映輸入變數,狀態變數和輸出變數間關係的一對向量方程,稱為狀態方程和輸出方程。線性系統的狀態空間理論自提出以來,已經得到了非常廣泛的研究,而在狀態空間描述的基礎上進行控制系統設計是狀態空間理論的一個重要組成部分。控制系統設計一般可分為兩類,一類是非優化型設計,其目的是針對某定常控制系統,設計某種形式的線性定常反饋控制律,使得閉環系統具有指定的期望的一組極點,這種設計以狀態反饋極點配置為代表。另一類設計是所謂的優化設計,即設計某種反饋控制律(線性或非線性),使得閉環系統的某種性能指標達到最優,這種設計方法以二次最優控制為代表。