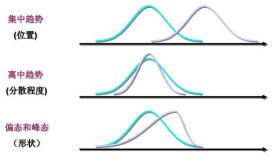
集中趨勢
表示機率分佈的中間值
集中趨勢又稱“數據的中心位置”、“集中量數”等。它是一組數據的代表值。集中趨勢的概念就是平均數的概念，它能夠對總體的某一特徵具有代表性，表明所研究的輿論現象在一定時間、空間條件下的共同性質和一般水平。就變數數列而言，由於整個變數數列是以平均數為中心而上下波動的，所以平均數反映了總體分佈的集中趨勢，它是表明總體分佈的一個重要特徵值。根據變數數列的平均數，就可以了解所研究總體的集中趨勢和一般特徵。集中趨勢是用來描述輿論現象的重要統計分析指標，常用的有平均數、中位數和眾數等，它們在不同類型的分佈數列中有不同的測定方法。
取得集中趨勢代表值的方法有兩種：數值平均數和位置平均數。
從總體各單位變數值中抽象出具有一般水平的量，這個量不是各個單位的具體變數值，但又要反映總體各單位的一般水平，這種平均數稱為數值平均數。數值平均數有算術平均數、調和平均數、幾何平均數等形式。
算術平均數：算術平均數就是觀察值的總和除以觀察值個數的商，是集中趨勢測定中最重要的一種，它是所有平均數中應用最廣泛的平均數。算術平均數分為簡單算術平均數和加權算術平均數。
調和平均數可以看成是變數χ的倒數的算術平均數的倒數，故有時也被稱為“倒數平均數”。調和平均數分為簡單調和平均數和加權調和平均數。
簡單調和平均數計算：
加權調和平均數計算：
簡單幾何平均數的計算：
加權幾何平均數的計算：
位置平均數就是根據總體中處於特殊位置上的個別單位或部分單位的標誌值來確定的代表值，它對於整個總體來說，具有非常直觀的代表性，因此，常用來反映分佈的集中趨勢。常用的有眾數、中位數。
眾數——是總體中出現次數最多的變數值，在實際工作中有時有它的特殊用途。
中位數——將數據按大小順序排列起來，形成一個數列，居於數列中間位置的那個數據就是中位數。
在統計學中，集中趨勢（central tendency）或中央趨勢，在口語上也經常被稱為平均，表示一個機率分佈的中間值。最常見的幾種集中趨勢包括算數平均數、中位數及眾數。集中趨勢可以由有限的數組（如一群樣本）中或理論上的機率分配（如正態分佈）中求得。有些人使用集中趨勢（或集中性）這個辭彙以表示“數量化的資料之中央值的趨勢”。在這種意義下，我們可以利用資料的離散程度（例如標準偏差或四分差等相似的統計量）判別其集中趨勢的程度。
集中趨勢（central tendency）一詞於1920年代後期出現。
在指數分配exp(λ)中，期望值為而中位數為，二者並不一致。
在左右對稱的機率分佈中，不同的集中趨勢統計量有相同結果，但在偏度遠離0時則可能不一致。在單峰型的機率分佈（unimodal probability distribution）中，平均數（μ）、中位數（ν）與眾數（θ）的關係。
基本信息
- 中文名
- 集中趨勢
- 別名
- 中央趨勢
- 外文名
- central tendency
- 術語類別
- 統計學
- 代表
- 值或中心值
- 測定方法
- 數值平均數