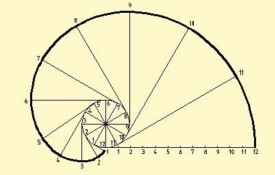
圓的漸開線

繩子端點的軌跡是一條曲線。抽象理解為繩子的直線叫做發生線。這條曲線叫做圓的漸開線。這個定圓叫做漸開線的基圓。

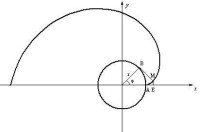
設基圓圓心為O，半徑為r，細繩外端的初始位置 為A。以O為原點，有向直線OA為x軸，建立平面直角坐標系。設M(x,y)是圓的漸開線上任一點，MB是⊙O的切線，B為切點，∠AOB=φ（弧度）是以OA為始邊，OB為終邊的正角。取φ為參數，圓的漸開線的參數方程是

x=r(cos φ+φsin φ)

y=r(sin φ-φcos φ)

圓的漸開線廣泛應用於齒輪的嚙合，齒輪的受力總是沿著與基圓相切的方向。

已知圓的直徑D，畫漸開線的方法首圖

(1)將圓周分成若干等分(圖中為12等分)，將周長πD作相同等分；

(2)過周長上各等分點作圓的切線；

(3)在第一條切線上，自切點起量取周長的一個等分（πD/12）得點1；在第二條切線上，自切點起量取周長的兩個等分（2xπD/12）得點2；依此類推得點3、4、……、12；

(4)用曲線板光滑連接點1、2、3、……、12。即得圓的漸開線。

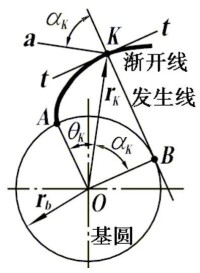
（1）漸開線的發生線滾過的距離等於其在基圓滾過的弧長。

（2）漸開線上任一點的法線恆與基圓相切。

（3）BK為漸開線K點的曲率半徑，漸開線距基圓越遠越平直。

（4）Fn與Vk之間所夾的銳角為K點處的壓力角。各點處壓力角大小不等。基圓上壓力角為零，距基圓越遠壓力角越大。

（5）基圓越小漸開線越彎曲；基圓半徑無窮大時漸開線為直線。

（6）基圓內無漸開線。