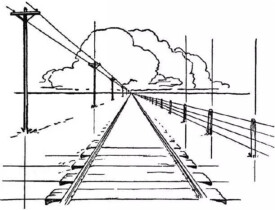
透視圖

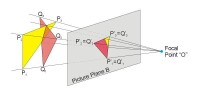
基面：形體所在的水平面，用字母G表示。基面相當於三投影面體系中的水平投影面H。

畫面：透視圖所在的平面，一般為鉛垂面，用字母P表示。也可以用傾斜平面做畫面。

基線：基面與畫面的交線，用字母gl表示。

視點：觀看者眼睛所在的位置，用字母S表示。

站點：觀看者站定的位置，即視點S的基面上的正投影，用E表示。

心點：視點S在畫面上的正投影，用字母Vc表示。

主視線：垂直於畫面P的視線，也就是過視點S和中心點Vc的直線。也叫中心視線。

視平面：過視點S的水平面。

透視圖

因為有了光我們才得以看到自然界中的一切，這個過程就是光線照射到物體上並通過眼球內水晶體把光線反射到我們眼內視網膜上而形成圖像，我們把光線在眼球水晶體的折射焦點叫做視點，視網膜上所呈現的圖像稱為畫面。只是人腦通過自身的機能處理將倒過來的圖像轉換成正立圖像。如果我們在眼前假定一個平面或放置一透明平面，以此來截獲物體反射到眼球內的光線，就會得到與實物一致的圖像，這個假定平面，也就是我們平時畫畫的畫面。

透視圖的基本畫法有很多種，我們常用的就是建築師法、量點法、距點法和網格法。

1）利用跡點和滅點確定直線的全線透視（直線的透視方向），然後再藉助視線的水平投影與基線的交點確定各點的透視位置，進而得出直線的透視長度的方法稱為建築師法。

2）由於要利用視線的水平投影確定透視位置，故建築師法畫透視圖時，必須將水平投影圖置於畫面的上方。

3）與視線跡點法相比，建築師法不需要在畫面上連接心點與各點的正面投影，故畫面上線條較少，圖面更清晰。

4）對於複雜建築形體，通常先將建築物的平面圖的透視（透視平面圖）畫出來，在此基礎上再將各部分的透視高度豎起來，從而得到整個透視。

5）因為不論按原基線、降低的基線或升高的基線所畫出的各個透視平面圖，其上相應頂點總是位於同一鉛垂線上，故實際作圖時通常拉大基線與視平線之間的距離以得出準確的透視交點。

1）與跡點結合，將平面圖中各直線線段的真實長度轉移到基線上，再利用量點確定各點的透視位置，進而得出其透視長度的作圖方法稱為量點法。

2）某一方向直線的透視長度，只能用對應的量點來求；每一方向的直線都有自己的滅點和量點；同方向直線共滅點和量點。

3）量點法畫的也是透視平面圖，在此基礎上豎高度才能得到完整透視。

4）應用量點法畫透視平面圖時，不需要將水平投影圖置於畫面的上方，因此可以擺脫水平投影圖的束縛。

與畫面垂直的畫面相交線的量點就稱為距點。

1）在繪製某一區域的建築群的鳥瞰圖或一些平面較複雜的建築物的透視圖或室內透視圖時，通常是利用網格法來解決的。因為這些描繪對象，其透視輪廓不是向一個或兩個滅點消失，而是多方向消失的。用前述各種方法繪製透視圖很不方便，甚至是不可能的。

2）網格法的作圖原理是首先將建築物或建築群的平面圖納入一個正方形的網格中來進行透視定位，畫出透視平面圖，然後求出各部分透視高度，以此畫出透視圖。

當視點、畫面和物體的相對位置不同時，物體的透視形象將呈現不同的形狀，從而產生了各種形式的透視圖。這些形式不同的透視圖，他們的使用情況以及所採用的作圖方法都不盡相同。習慣上，可按透視圖上滅點的多少來分類和命名，也可根據畫面、視點和形體之間的空間關係來分類和命名。不管怎麼樣分類和命名，透視圖都分為以下三類。

建築物只有一個方向的輪廓線垂直於畫面，其滅點就是主點；而另兩個方向的輪廓線均平行於畫面，沒有滅點。這時畫出的透視，稱為一點透視。

兩點透視

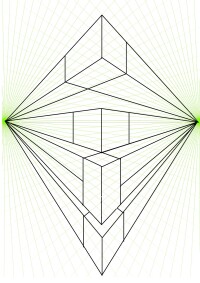
如果建築物只有鉛垂的輪廓線平行於畫面，而另兩組水平的輪廓線均與畫面斜交，於是在畫面上就會得到兩個滅點，這兩個滅點都在視平線上。這時畫出的透視，稱為兩點透視。

如果畫面傾斜於基面，即畫面與建築物的三組主要方向的輪廓線都相交，於是畫面上就會形成三個滅點。這時我們畫出的透視圖，稱為三點透視，又稱為斜透視。參數的選擇

透視圖是在人眼可視的範圍內。在透視圖上，因投影線不是互相平行集中於視點，所以顯示物體的大小，並非真實的大小，有近大遠小的特點。形狀上，由於角度因素，長方形或正方形常繪成不規則四邊形，直角繪成銳角或鈍角，四邊不相等。圓的形狀常顯示為橢圓。

透視圖是以作畫者的眼睛為中心作出的空間物體在畫面上的中心投影（而非平行投影）。它具有將三維空間物體轉換或便於表面到畫面上的二維圖像的作用。

我們常把經典透視圖分為一點透視,兩點透視和三點透視，它們之間的區別在於對象的3個主視方向與投影平面的平行個數。

透視圖

透視圖

術語解釋

透視產生

基本畫法

建築師法

量點法

距點法

網格法

分類

分類依據

一點透視

兩點透視

三點透視

基本信息