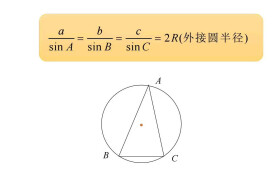
正弦定理

在任意△ABC中，角A、B、C所對的邊長分別為a、b、c，三角形外接圓的半徑為R，直徑為D。則有：

一個三角形中，各邊和所對角的正弦之比相等，且該比值等於該三角形外接圓的直徑（半徑的2倍）長度。

早在公元2世紀，正弦定理已為古希臘天文學家托勒密(C．Ptolemy)所知．中世紀阿拉伯著名天文學家阿爾·比魯尼(al—Birunj，973一1048)也知道該定理．但是，最早清楚地表述並證明該定理的是13世紀阿拉伯數學家和天文學家納綏爾丁。在歐洲，猶太數學家熱爾松在其《正弦、弦與弧》中陳述了該定理：“在一切三角形中，一條邊與另一條邊之比等於其對角的正弦之比”，但他沒有給出清晰的證明。15世紀，德國數學家雷格蒙塔努斯在《論各種三角形》中給出了正弦定理，但簡化了納綏爾丁的證明。1571年，法國數學家韋達(F．Viete，1540一1603)在其《數學法則》中用新的方法證明了正弦定理，之後，德國數學家畢蒂克斯(B．Pitiscus，1561—1613)在其《三角學》中沿用韋達的方法來證明正弦定理。

歷史上，正弦定理的幾何推導方法豐富多彩。根據其思路特徵，主要可以分為兩種。

第一種方法可以稱為“同徑法”，最早為13世紀阿拉伯數學家、天文學家納綏爾丁和15世紀德國數學家雷格蒙塔努斯所採用。“同徑法”是將三角形兩個內角的正弦看作半徑相同的圓中的正弦線（16世紀以前，三角函數被視為線段而非比值），利用相似三角形性質得出兩者之比等於角的對邊之比。納綏爾丁同時延長兩個內角的對邊，構造半徑同時大於兩邊的圓。雷格蒙塔努斯將納綏爾丁的方法進行簡化，只延長兩邊中的較短邊，構造半徑等於較長邊的圓。17~18世紀，中國數學家、天文學家梅文鼎和英國數學家辛普森各自獨立地簡化了“同徑法”。

18世紀初，“同徑法”又演化為“直角三角形法”，這種方法不需要選擇並作出圓的半徑，只需要作出三角形的高線，利用直角三角形的邊角關係，即可得出正弦定理。19世紀，英國數學家伍德豪斯開始統一取R=1，相當於用比值來表示三角函數，得到今天普遍採用的“作高法”。

第二種方法為“外接圓法”，最早為16世紀法國數學家韋達所採用。韋達沒有討論鈍角三角形的情形，後世數學家對此作了補充。

△ABC中，若角A，B，C所對的邊為a，b，c，三角形外接圓半徑為R，直徑為D，正弦定理進行變形有

1. （齊次式化簡）

2. , ,

3.

4.（等比，不變）

5. （三角形面積公式）

正弦定理指出了任意三角形中三條邊與對應角的正弦值之間的一個關係式。由正弦函數在區間上的單調性可知，正弦定理非常好地描述了任意三角形中邊與角的一種數量關係。

一般地，把三角形的三個角A、B、C和它們的對邊a、b、c叫做三角形的元素。已知三角形的幾個元素求其他元素的過程叫做解三角形。正弦定理是解三角形的重要工具。

在解三角形中，有以下的應用領域：

● 已知三角形的兩角與一邊，解三角形。

● 已知三角形的兩邊和其中一邊所對的角，解三角形。

● 運用a:b:c=sinA:sinB:sinC解決角之間的轉換關係。

只需證明任意三角形內，任一角的邊與它所對應的正弦之比值為該三角形外接圓直徑即可。

現將△ABC，做其外接圓，設圓心為O。我們考慮∠C及其對邊AB。設AB長度為c。

1.若∠C為直角，則AB就是⊙O的直徑，即c= 2r。

∵ （特殊角正弦函數值）

∴

2.若∠C為銳角或鈍角，過B作直徑BC`'交 ⊙O於C`，連接C'A，顯然BC'= 2r=R。

若∠C為銳角，則C'與C落於AB的同側，

此時∠C'=∠C（同弧所對的圓周角相等）

∴在Rt△ABC'中有

若∠C為鈍角，則C'與C落於AB的異側，此時∠C'+∠C=180°，sin C'=sinC，亦可推出。

考慮同一個三角形內的三個角及三條邊，同理，分別列式可得。故對任意三角形，定理得證。

若△ABC為銳角三角形，過點A作單位向量j⊥ ,則j與 的夾角為90°-∠A,j與的夾角為90°-∠C.由向量的加法原則可得

為了與圖中有關角的三角函數建立聯繫，我們在上面向量等式的兩邊同取與向量j的數量積運算，得到

∴|j| | | Cos90°+|j| | | Cos(90°-C)=|j| | |Cos(90°-A)

.∴asinC=csinA 即

同理，過點C作與 垂直的單位向量j,則j與 的夾角為90°+∠C,j與 的夾角為90°+∠B,

可得

若△ABC為鈍角三角形，不妨設A>90°,過點A作與AB垂直的單位向量j,則j與AC的夾角為∠A-90°,j與CB的夾角為90°+∠B.同理

a·Cos(90°-B)=b·Cos(A-90°),

∴asinB=bsinA 即

過點C作與 垂直的單位向量j,則j與 的夾角為90°+∠C,j與 的夾角為90°+∠B,可得

綜上，

解三角形時，已知兩角與一邊，三角形是確定的，利用正弦定理解三角形時，其解是唯一的；已知三角形的兩邊和其中一邊的對角，由於該三角形具有不穩定性，所以其解不確定，可結合平面幾何作圖的方法及“大邊對大角，大角對大邊”定理和三角形內角和定理去考慮解決問題。

一般地，已知兩邊和其中一邊的對角解三角形，有兩解、一解、無解三種情況，可參考三角形性質、鈍角三角形性質進行判斷。若已知A、A的對邊a、A與a的夾邊C，則：

對於鈍角三角形，

● 若a≤b，則無解；

● 若a>b，則有一解；

對於銳角三角形，

● 若a

● 若a=bsinA，則有一解；

● 若bsinA

● 若a≥b，則有一解。

● 如果這個三角形無解，那麼沒有圓弧能通過這個三角形。