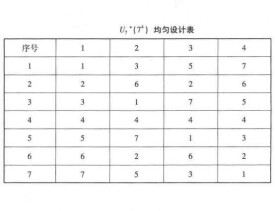
均勻設計表
均勻設計表
均勻設計表是根據數論在多維數值積分的應用原理,仿照正交表構造的具有均勻性的一種規格化陣列表,用於均勻試驗設計,均勻設計表是利用同餘法則建立起來的。一般用Un(m)表法,其中U表示均勻設計表;n表示行數(所需均勻試驗次數);m表示每列中不同字碼的個數(可容納的因子水平數);r表示列數 (最多能安排的因子個數) 。
均勻設計和正交設計很相似,也是通過一套精心設計的表來進行實驗設計的。表1為均勻設計表。表2為均勻設計表。這兩個表比較常見。
| 表1 | ||||||
|---|---|---|---|---|---|---|
| 序號 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
| 表2 | ||||||
|---|---|---|---|---|---|---|
| 序號 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 |
每一個均勻設計表用一個符號或表示,其中U表示均勻設計,n表示要做的實驗次數,q表示每個因素的水平數,m表示該表的列數。右上角加“”和不加“”代表兩種不同類型的均勻設計表。通常加“”的均勻設計表有更好的均勻性,應該優先選用。例如表示要做6次實驗,每個因素有六個水平,由4列組成的均勻設計表。
每個均勻設計表都附有一個使用表,它指示我們如何從設計表中選擇適當的列。
下面是一張均勻設計表和相應的使用表:
| 表3 | ||||
|---|---|---|---|---|
列號 試驗號 | 1 | 2 | 3 | 4 |
1 2 3 4 5 | 1 2 3 4 5 | 2 4 1 3 5 | 3 1 4 2 5 | 4 3 2 1 5 |
| 表4 | ||||
|---|---|---|---|---|
| 因子數 | 入選列號 | |||
| 2 | 1 | 2 | ||
| 3 | 1 | 2 | 4 | |
| 4 | 1 | 2 | 3 | 4 |
的使用方法,若試驗兩個因子,則選第1和第2列;若試驗三個因子,則選第1,2,4列……
表5是的使用表,它告訴我們,若有兩個因素,應選用1、3兩列來安排實驗;若有三個因素,應選用1、2、3三列……
| 表5 | ||||||
|---|---|---|---|---|---|---|
| 因子數 | 列 號 | |||||
| 2 | 1 | 3 | ||||
| 3 | 1 | 2 | 3 | |||
| 4 | 1 | 2 | 3 | 6 | ||
| 5 | 1 | 2 | 3 | 4 | 6 | |
| 6 | 1 | 2 | 3 | 4 | 5 | 6 |
當實驗次數n給定時,通常U表比U 表能安排更多的因素。故當因素s較大,且超過U 的使用範圍時可使用U表。
均勻設計有其獨特的排布實驗點的方式,其特點表現在:
(1) 每個因素的每個水平做1次且僅做1次實驗;
(2) 任兩個因素的實驗點在平面格子點上,每行每列有且僅有一個實驗點。如表的第1列和第3列構成的實驗點如圖1所示。

圖1

圖2
特點(1)和(2)反映了實驗點安排的均衡性,即對各因素以及每個因素的每個水平一視同仁。
(3) 均勻設計表中任兩列組成的實驗方案一般並不等價。例如用的1、3和1、6列分別畫圖,得到圖1和圖2。我們看到,圖1的點散布比較均勻,而圖2的點散布並不均勻。均勻設計表的這一特點和正交表有很大的不同,因此,每個均勻設計表必須有一個附加的使用表。
(4)當因素的水平數增加時,均勻設計的實驗次數按水平數的增加量增加,如水平數從9增加到10,實驗次數n也從9增加到10。而當正交設計水平數增加時,實驗次數按水平數的平方增加,水平數從9增加到10,實驗次數從81增加到100。由於這個特點,使均勻設計更便於安排水平數較多的實驗。
利用均勻設計表來安排實驗,其步驟和正交設計很相似,但也有一些不同之處。通常有如下步驟:
(1) 根據實驗的目的,選擇合適的因素和相應的水平。
(2)選擇適合該實驗的均勻設計表,然後根據該表的使用表從中選出列號,將因素分別安排到這些列上,並將這些因素的水平按所在列的指示分別對號。
(A) 原料配比: 1.0,1.4, 1.8, 2.2,2.6,3.0,3.4;
(B)吡啶量(cm ): 10,13,16,19,22,25, 28;
(C)反應時間(h): 0.5,1.0,1.5, 2.0,2.5,3.0, 3.5。
根據因素和水平,我們選取均勻設計表。從它的使用表中可以查到,當因素數等於三時,將A、B、C分別放在表的前3列。
根據實驗方案進行實驗,其收率(Y)列於表6的最後一列。其中以第7號實驗的結果為最好,其工藝條件為配比3.4,吡啶量28cm ,反應時間3. 5h。
| 表6 製備阿魏酸的實驗方案和結果 | ||||
|---|---|---|---|---|
| 序號 | 配比(A) | 吡啶量(B) | 反應時間(C) | 收率(Y) |
| 1 | 1.0(1) | 13(2) | 1.5(3) | 0.330 |
| 2 | 1.4(2) | 19(4) | 3.0(6) | 0.336 |
| 3 | 1.8(3) | 25(6) | 1.0(2) | 0.294 |
| 4 | 2.2(4) | 10(1) | 2.5(5) | 0.476 |
| 5 | 2.6(5) | 16(3) | 0.5(1) | 0.209 |
| 6 | 3.0(6) | 22(5) | 2.0(4) | 0.451 |
| 7 | 3.4(7) | 28(7) | 3.5(7) | 0.482 |
註:表中括弧內數字為均勻設計表中對應的水平代號,下同。
回歸分析是數據分析的有力工具,它能揭示變數之間的相互關係,因此在均勻設計的數據分析中成為主要的手段。
例2 試用線性回歸模型來擬合表6中的實驗數據。
解:
設線性回歸方程為:
均勻設計表
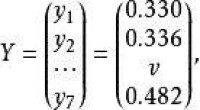
均勻設計表
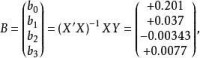
均勻設計表
於是得到回歸方程:
此回歸方程是否成立,需用方差分析法進行假設檢驗。但檢驗過程的計算量太大,過於煩瑣,此處不予討論。
下面介紹均勻設計表的構造,這對於正確理解和使用均勻設計有很大幫助。
均勻設計表是利用同餘運算生成的,因此先介紹同餘運算。設a、b均為自然數,其中b=1、2、3、4、..n,n稱為b的模。b與a的同餘運算定義如下:
均勻設計表
每一個均勻設計表都是一個n行m列的矩陣,每一列都是1、2、..n這n個自然數的重新排列。表的第一行是1、2、...的一個子集。