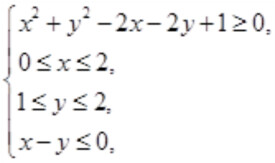不等式組
用不等號連接的式子
用“大於號”、“小於號”、“不等號”、“大於等於”或“小於等於”連接並具有大小關係的式子,叫做不等式。
關於x的不等式組:
x
的所有整數解的和是-7,則m的取值範圍是
解答:
先移項:
然後解出
又因為滿足且x
解不等式組,可以先把其中的不等式逐條算出各自的解集,然後分別在數軸上表示出來。
以兩條不等式組成的不等式組為例,
①若兩個未知數的解集在數軸上表示同向左,就取在左邊的未知數的解集為不等式組的解集,此乃“同小取小”
②若兩個未知數的解集在數軸上表示同向右,就取在右邊的未知數的解集為不等式組的解集,此乃“同大取大”
③若兩個未知數的解集在數軸上相交,就取它們之間的值為不等式組的解集。若x表示不等式的解集,此時一般表示為a
④若兩個未知數的解集在數軸上向背,那麼不等式組的解集就是空集,不等式組無解。此乃“向背取空”
學習步驟
1.了解一元一次不等式及其相關概念,經歷“把實際問題抽象為不等式”的過程,能夠“列出不等式或不等式組表示問題中的不等關係”,體會不等式(組)是刻畫現實世界中不等關係的一種有效的數學模型。
2.通過觀察、對比和歸納,探索不等式的性質,能利用它們探究一元一次不等式的解法。
3.了解解一元一次不等式的基本目標(使不等式逐步轉化為或x)
4.了解不等式組及其相關概念,會解由兩個一元一次不等式組成的不等式組,並會用數軸確定解集。
5.通過課題學習,以體育比賽問題為載體,探究實際問題中的不等關係,進一步體會利用不等式解決問題的基本過程(見上頁圖),感受數學的應用價值,提高分析問題、解決問題的能力。
6.不等式組問題主要與不空不滿型的以及至少,至多等。在實際生活中運用較廣,應該多實踐,多運用,提高自身數學能力
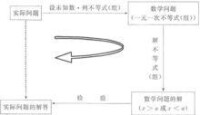
不等式組
不等式——應用題的一般步驟
1、審:審清題意,弄懂已知什麼,求什麼,以及各個數量之間的關係。
2、設:只能設一個未知數,一般是與所求問題有直接關係的量。
3、找:找出題中所有的不等關係,特別是隱含的數量關係。
4、列:列出不等式組。
5、解:分別解出每個不等式的解集,再求其公共部分,最後得出結果。
6、答:根據所得結果作出回答。