拉普拉斯定理
拉普拉斯定理
徠設在獨立試驗序列中,事件A在各次試驗中發生的概率為p(0
則有:
其中z為任意實數,.
證:設隨機變數ξ^i表示事件A在第i次試驗中發生的次數,則ξ^i服從“”分佈,且有:
直接由列維定理就得此定理。
在上述定理條件下,當n充分大時,η^n落在m₁與m₂之間的概率
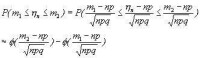 拉普拉斯定理 |
註:此定理實際上說明了當n充分大時,二項分佈B(n,p)逼近正態分佈N(np,npq),這是因為η^n是服從二項分佈B(n,p)的。
例 某批產品的次品率為0.005,試求不多於70件的概率P。
解 設ξ表示在任意抽取的10000件產品中的次品數,則ξ服從二項分佈B(10000,0.005)。此時若直接計算概率
這是較困難的。我們利用近似公式來計算,則
已知,
,故
拉普拉斯定理
