Feistel
Feistel
Feistel 密碼結構,在密碼學研究中,Feistel 密碼結構是用於分組密碼中的一種對稱結構。以它的發明者 Horst Feistel 為名,而Horst Feistel 本人是一位物理學家兼密碼學家,在他為 IBM 工作的時候,為Feistel 密碼結構的研究奠定了基礎。很多密碼標準都採用了Feistel 結構,其中包括DES。Feistel 的優點在於:由於它是對稱的密碼結構,所以對信息的加密和解密的過程就極為相似,甚至完全一樣。這就使得在實施的過程中,對編碼量和線路傳輸的要求就減少了幾乎一半。
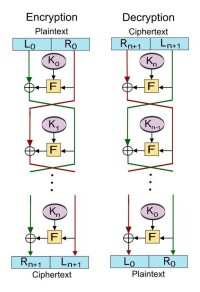
Feistel 密碼結構

Feistel 的加密解密過程
(1)將明文信息均分為兩塊:(L0,R0);
(2)在每一輪中,進行如下運算(i 為當前輪數):
L = Ri;
R = Li ⊕F (Ri,Ki)。(其中⊕為異或操作)
所得的結果即為:(R,L)。
對於密文(R,L),我們將i 由n 向0 進行,即, i = n,n-1,……,0。然後對密文進行加密的逆向操作,如下:
(1)Ri = L;
(2)Li = R⊕F (Li+1,Ki)。(其中⊕為異或操作)
所得結果為(L0,R0),即原來的明文信息。
影響Feistel 結構的因素有如下5 個:
(1)塊的大小:大的塊會提高加密的安全性,但是會降低加密、解密的速度。截止至2013年,比較流行的這種方案是64 bit。而128 bit 的使用也比較廣泛。
(2)密鑰的大小:同上。現在流行的是64 bit ,而 128 bit 正逐漸成為主流。
(3)循環次數(輪次數):每多進行一輪循環,安全性就會有所提高。現階段比較流行的是16輪。
(4)子密鑰的生成演演算法:生成演演算法越複雜,則會使得密碼被破譯的難度增強,即,信息會越安全。
(5)輪函數的複雜度:輪函數越複雜,則安全性越高。