關聯矩陣
關聯矩陣
關聯矩陣法是常用的系統綜合評價法,它主要是用矩陣形式來表示每個替代方案有關評價指標及其重要度和方案關於具體指標的價值評定量之間的關係特點是:它使人們容易接受對複雜系統問題的評價思維過程數學化,通過將多目標問題分解為兩指標的重要度對比,使評價過程簡化、清晰。
關聯矩陣即用一個矩陣來表示各個點和每條邊之間的關係。
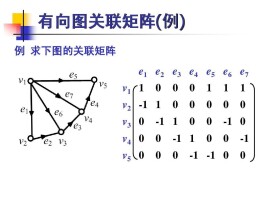
對於一個無向圖G,pxq, p為頂點的個數,q為邊數。bij 表示在關聯矩陣中點i和邊j之間的關係。若點i和邊j之間是連著的,則bij = 1. 反之,則bij = 0. 例如:
關聯矩陣
需要注意的一點,每一行值的總和為該點的度。
對於有向圖,若bij = 1,表示邊j離開點i。若bij = -1,表示邊j進入點i。若bij = 0,表示邊j和點i不相關聯。
應用關聯矩陣法的關鍵,在於確定每個評價指標的相對重要度(即權重Wj)以及根據評價主體給定的評價指標的評價尺度,確定方案關於評價指標的價值評定量(Vij)。
關聯矩陣法是因其整個程序如同一個矩陣排列而得名。關聯矩陣法是對多目標系統方案從多個因素出發綜合評定優劣程度的方法,是一種定量與定性相結合的評價方法,它用矩陣形式來表示各替代方案有關評價指標的評價值,然後計算各方案評價值的加權和,再通過分析比較,確定評價值加權和最大的方案即為最優方案。
而顯著不同之處在於指標確定的同時賦予權重,即對其各評估要素依據其對於被評估者的重要程度的差異進行區別對待,從而使得定性指標的量化更加科學可靠。
其分析的一般步驟如下:
評估內容指標化是定量評估的基本要求。評估指標體系在結構上具有層次性。一般的評估量表由兩至三個層次的指標構成:
(1)指標模塊。不同方案的評估量表的模塊內容可以不一樣,根據評估內容復蓋面的差異,指標模塊也可以根據需要分成不同的模塊.
(2)一級指標,又稱為指標項目.
(3)二級指標,是一級指標模塊的進一步細分而得來的。有些複雜的量表還包括第三級指標。
在指標體系中,各個指標對於方案(評價主體)的重要程度是不同的,這種重要程度的差別需要通過在各指標中分配不同的權重來體現。一組評價指標所相對應的權重組成了權重體系.
任何一組權重{Wi/i=1,2,…,n}體系必須滿足下述兩個條件:
推算過程
推算過程
通常有以下兩種方法:
(1)專家評定法:由專家打分,去掉最低分和最高分,取算術平均值。
(2)德爾菲函詢法:利用專家的知識和長期積累的經驗,減輕權威的影響。
在一層指標體系中,評估者對被評估者作出的評估值為:則其對應的權重體系{Wij/i=1,2,…,n;j=1,2,…,m}應滿足:
推算過程
此方法應用於多目標系統。它是用矩陣形式來表示各替代方案有關評價項目的評價值。然後計算各方案評價值的加權和,在通過分析比較,綜合評價值——評價值加 權和最大的方案即為最優方案。應用關聯矩陣法的關鍵在於確定各評價指標的相對重要度,即權重,以及由評價主體給定的評價指標的評價尺度。
它的應用過程是:根據不同類型人員,確定不同的指標模塊(又稱一級指標),然後將指標模塊分解獲得二級指標(有些複雜的量表還包括三級指標),建立起具有層次結構的評估。這是它與一般的因素評分法的相同之處,而顯著不同之處在於指標確定的同時賦予權重,即對其各評估要素依據其對於被評估者的重要程度的差異進行區別對待,從而使得定性指標的量化更加科學可靠。關聯矩陣法的基本出發點是建立評價及分析的層次結構,在權重的確定上,關聯矩陣法要來得簡單,操作性強.它是根據具體評價系統,採用矩陣形式確定系統評價指標體系及其相應的權重,然後對評價系統的各個方案計算其綜合評價值——各評價項目評價值的加權和。
關聯矩陣法的特點是:它使人們容易接受對複雜系統問題的評價思維過程數學化,通過將多目標問題分解為兩指標的重要度對比,使評價過程簡化、清晰。
應用關聯矩陣法的關鍵在於確定各評價指標的權重Wi以及由評價主體給定的評價指標的評價尺度確定方案關於評價指標的價值評定量(Vij)。目前確定權重和評價尺度還沒有普遍適用的方法,較為常用的有逐項比較法和A·古林法(KLEE法),前者較為簡便,後者在對各評價項目間的重要性要作出定量估計時顯得更為有效。
關聯矩陣法最大的特點是引進了權重概念,對各評估要素在總體評價中的作用進行了區別對待。