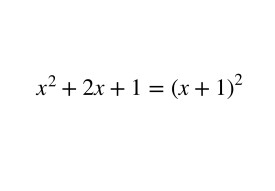分解

初等數學中，把多項式的分解叫因式分解，其一般步驟為：一提二套三分組。要求將多項式分到不可再分的形式。

一個多項式要能分解因式，則結果唯一。因為：數域F上的次數大於零的多項式f(x),如果不計零次因式的差異，那麼f(x)可以唯一的分解為以下形式：*,其中α是f(x)的最高次項的係數，是首1互不相等的不可約多項式，並且Pi(x)(I=1,2…,t)是f(x)的Ki重因式。（*）或叫做多項式f(x)的典型分解式。

如果多項式各項都有公共因式，則可先考慮把公因式提出來，即用提公因式法進行因式分解，注意要每項都必須有公因式。

例：

多項式如果滿足特殊公式的結構特徵，即可採用套公式法，進行多項式的因式分解，故對於一些常用的公式要求熟悉，除教材的基本公式外，數學競賽中常出現的一些基本公式現整理歸納如下：

a²-b²=(a+b)(a-b)

a²±2ab+b²=(a±b)²

a³+b³=(a+b)(a²-ab+b²)

a³-b³=(a-b)(a²+ab+b²)

a³±3a²b+3ab²±b²=(a±b)³

a²+b²+c²+2ab+2bc+2ac=(a+b+c)²

a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-ac-bc)

(n為奇數)

說明由因式定理，即對一元多項式f(x)，若f(b)=0，則一定含有一次因式x-b。可判斷當n為偶數時，當a=b,a=-b時，均有aⁿ-bⁿ=0故aⁿ-bⁿ中一定含有a+b，a-b因式。

注多項式分解時，先構造公式再分解。

當多項式的項數較多時，可將多項式進行合理分組，用分組分解法達到順利分解的目的。當然可能要綜合其他分法，且分組方法也不一定唯一。

對於形如ax²+bx+c結構特徵的二次三項式可以考慮用十字相乘法,

即x²+(b+c)x+bc=(x+b)(x+c)當x²項係數不為1時，同樣也可用十字相乘進行操作。

註：“ax⁴+bx²+c”型也可考慮此種方法。

在分解二次三項式時，十字相乘法是常用的基本方法，對於比較複雜的多項式，尤其是某些二次六項式，如4x²-4xy-3y²-4x+10y-3，可以運用雙十字相乘法分解因式，其具體步驟為：

（1）用十字相乘法分解由前三次組成的二次三項式，得到一個十字相乘圖

（2）把常數項分解成兩個因式填在第二個十字的右邊且使這兩個因式在第二個十字中交叉之積的和等於原式中含y的一次項，同時還必須與第一個十字中左端的兩個因式交叉之積的和等於原式中含x的一次項。

例：(ab+a)+(b²-b-2)=a(b+1)+(b+1)(b-2)=(b+1)(a+b-2)

對於一些多項式，如果不能直接因式分解時，可以將其中的某項拆成二項之差或之和。再應用分組法，公式法等進行分解因式，其中拆項、添項法不是唯一，可解有許多不同途徑，對題目一定要具體分析，選擇簡捷的分解方法。

換元法就是引入新的字母變數，將原式中的字母變數換掉化簡式子。運用此種方法對於某些特殊的多項式因式分解可以起到簡化的效果。

待定係數法是解決代數式恆等變形中的重要方法，如果能確定代數式變形后的字母框架，只是字母的係數高不能確定，則可先用未知數表示字母係數，然後根據多項式的恆等性質列出n個含有特殊確定係數的方程(組)，解出這個方程(組)求出待定係數。待定係數法應用廣泛，在此只研究它的因式分解中的一些應用。

分解因式的方法是多樣的，且其方法之間相互聯繫，一道題很可能要同時運用多種方法才可能完成，故在知曉這些方法之後，要注意各種方法靈活運用。

順帶一提，梅森合數分解已經取得一些微不足道的進展：

1、p=4r+3，如果8r+7也是素數，則：；

例如：;11=4×2+3；

47|(2^23-1);47=4×11+3；

;83=4×20+3；

2、,則，

例如：;37=2×2×3×3+1；

；73=2×2×2×3×3+1；

;577=2×2×2×2×2×2×3×3+1；

3、,則；

例如：；29=2×3×5-1；

；179=2×2×3×3×5-1；

；239=2×2×2×2×3×5-1；

還有一些梅森數分解取得進展，不再一一敘述。