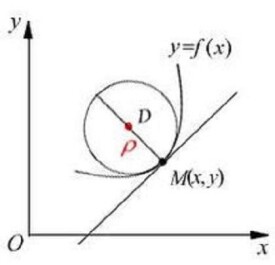
曲率半徑

曲率半徑主要是用來描述曲線上某處曲線彎曲變化的程度，特殊的如：圓上各個地方的彎曲程度都是一樣的故曲率半徑就是該圓的半徑；直線不彎曲，和直線在該點相切的圓的半徑可以任意大，所以曲率是0，故直線沒有曲率半徑，或記曲率半徑為∞。

圓形半徑越大，彎曲程度就越小，也就越近似於一條直線。所以說，曲率半徑越大麴率越小，反之亦然。

如果對於某條曲線上的某個點可以找到一個與其曲率相等的圓形，那麼曲線上這個點的曲率半徑就是該圓形的半徑（注意，是這個點的曲率半徑，其他點有其他的曲率半徑)。也可以這樣理解：就是把那一段曲線儘可能地微分，直到最後近似為一個圓弧，此圓弧所對應的半徑即為曲線上該點的曲率半徑。

在空間曲線的情況下，曲率半徑是曲率向量的長度。在平面曲線的情況下，則R要取絕對值。

其中s是曲線上固定點的弧長，φ是切向角，κ是曲率。

如果曲線以笛卡爾坐標表示為，則曲率半徑為（假設曲線可微分）

如果曲線由函數 和 參數給出，則曲率半徑為

實際上，這個結果可以解釋為

這裡。

如果 是 中的參數曲線，則曲線各點處的曲率半徑 由下式給出：

作為特殊情況，如果f（t）是從R到R的函數，則其圖的曲率半徑是

對於上半平面半徑a的半圓：

對於上半平面半徑a的半圓：

半徑a的圓的曲率半徑等於a。

在具有長軸2a和短軸2b的橢圓中，長軸上的頂點具有任何點的最小曲率半徑， ；

並且短軸上的頂點具有任何點的最大麴率半徑。

（1）對於差分幾何上的應用，請參閱Cesàro方程；

（2）對於地球的曲率半徑（由橢圓橢圓近似），請參見地球的曲率半徑；

（3）曲率半徑也用於梁的彎曲三部分方程中；

（4）曲率半徑（光學）。

（5）半導體結構中的應力：

涉及蒸發薄膜的半導體結構中的應力通常來自製造過程中的熱膨脹（熱應力）。發生熱應力是因為膜沉積通常在室溫以上。在從沉積溫度冷卻至室溫時，基板和膜的熱膨脹係數的差異引起熱應力。

當原子沉積在基底上時，由薄膜中形成的微觀結構引起固有應力。由於原子穿過空隙有吸引力的相互作用，薄膜中的微孔產生拉伸應力。

薄膜半導體結構中的應力導致晶片的翹曲。應力結構的曲率半徑與結構中的應力張量有關，可以用修正的Stoney公式來描述。可以使用光學掃描儀測量包括曲率半徑的應力結構的形貌。現代掃描儀工具具有測量基板全貌和測量兩個主曲率半徑的能力，同時為90米及以上的曲率半徑提供0.1%的精度。