大圓

大圓是球面幾何的基礎知識，被定義為過球心的平面和球面的交線。如果平面不過球心，則它和球面的交線定為小圓。大圓的圓心與球心重合，半徑與球的半徑相等。

球面上兩點的最小距離為經過兩點的大圓的劣弧。航海與航空中利用這一原理而設置了大圓航線。

1）大圓的平面過球心，大圓的圓心即球心；

2）大圓把球和球面分成相等的兩部分；

由於大圓的圓平面通過球心，大圓把球分成兩部分。我們設想將一部分球翻轉，嵌入另一部分中，使其底面重合。因為球面上所有的點與球心的距離都相等，所以一部分球面上的所有點都和另一部分球面上的所有對應點重合。因此，大圓把球和球面分成相等的兩部分。

3）兩個大圓平面的交線是球的直徑也是兩個大圓的直徑；

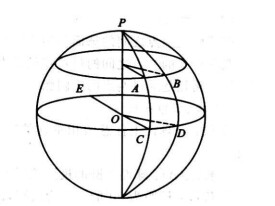
如右圖，弧ABEF和弧CDEF是任意兩個大圓，因為大圓平面都通過球心，所以球心O既在大圓平面ABEF上也在大圓平面CDEF上，即必在這兩個大圓平面的交線EF上。因為球心O也是大圓圓心，所以，通過球心O的兩個大圓平面的交線，既是球的直徑，也是這兩個大圓的直徑。

4）過球面上不在同一直徑上兩點，只能做一個大圓；

如左圖，A和B是球面上不在同一直徑兩端的兩個點，它們和球心O是不在同一直線上的三個點，由立體幾何知識知：過不在同一直線的三個點，能作且只能作一個平面，所以通過球面上不在同一直徑上兩點，只能做一個大圓。

5）過球面上在同一直徑上兩點，可以做無數個大圓。

在同一直徑兩端的兩個點和球面上任意一個第三點構成的平面都通過球心，所以能作無數個大圓。