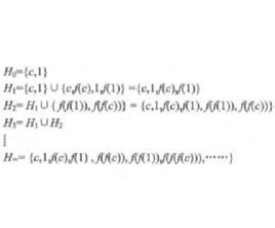海伯倫域
海伯倫域
設謂詞公式G的子句集為S,則按下述方法構造的個體變元域H稱為公式G或子句集S的海伯倫域(Herbrand域,簡稱H域):(1)令H0是S中所出現的常量的集合。若S中沒有常量出現,就任取一個常量a∈D,規定H0=a。(2)令Hi+1=Hi∪{S中所有的形如f(t1,...,tn)的元素),其中f(t1,...,tn)是出現於G中的任一函數符號,而t1,...,tn是Hi中的元素。i=0,1,2,…。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
子句集S中的基礎子句的項(常元)構成S的 海伯倫域(Herbrand域,簡稱H域,Herbrand Universes),構成方法如下:令F是出現在S中的函數符號的集合,除非F包含的所有函數符號均為0階(這時公式退化為常量的集合),否則,F是集合,其中表示S中的常元,,D是一個個體域:F是函數構成的表達式的集合,是的映射。S的H域是所有項的集合,。
由於F的階可超窮增加,因此,H域是一個可數超窮集。
海伯倫域
海伯倫域
海伯倫域
例1 求的H城,是解釋的常元,是變元。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
例2求命題的子句集的H域。
海伯倫域
海伯倫域
海伯倫域
(是常元)
海伯倫域
海伯倫域
海伯倫域
海伯倫域
(最外層的中有n個)
海伯倫域
海伯倫域
海伯倫域
即的H域。
海伯倫域
海伯倫域
Herbrand化(H化) 子句(或文字A,或原子A)的所有變元均被H域的元素替換,這一過程稱為H化,H化的結果稱為一個H化基例,也稱為H化基子句 (或H化基文字,或H化基原子)。
海伯倫域
海伯倫域
例3,的H化的若干結果是
海伯倫域
海伯倫域
海伯倫域
現在考慮對子句結構進行進一步的細化分析。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
(1)從非空的項變元取值範圍D內為每個項變元指定一個元素,即{公式G的項變元}→D;
海伯倫域
海伯倫域
第(1)步稱為半解釋。後面對其他非空域進行變元的賦值也稱為相應域的半解釋。
定義1不含有任何連接詞的謂詞公式叫 原子公式,簡稱 原子,而原子或原子的否定統稱 文字。
定義2子句就是由一些文字組成的析取式。
海伯倫域
定義4由子句構成的集合稱為 子句集。
定義5設謂詞公式G的子句集為S,則按下述方法構造的個體變元域H稱為公式G或子句集S的 Herbrand域,簡稱 H域。
海伯倫域
海伯倫域
(1)令H是S中所出現的常量的集合。若S中沒有常量出現,就任取一個常量,規定。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
(2)令{S中所有的形如的元素),其中是出現於G中的任一函數符號,而是中的元素。i=0,1,2,…。
定義6下列集合稱為子句集S的 原子集:
海伯倫域
海伯倫域
海伯倫域
其中,是出現在S中的任一謂詞符號,而則是S的H域上的任意元素。
定義7將沒有變元出現的原子、文字、子句和子句集分別稱作 基原子、基文字、基子句和 基子句集。
定義8當子句集S中的某個子句C中的所有變元符號均以其H域中的元素替換時,所得到的基子句稱作C的一個 基例。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
定義9 (可滿足性、不可滿足性)對於一個變元自由的一階語言公式G,如果至少存在一個D論域上的一個解釋,在此解釋下G為真,則稱G是 可滿足的,即;反之,如果對於任何解釋G均為假,則稱G是 不可滿足的,即,或。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
對於一個變元自由的一階語言公式集,即,如果至少存在一個D的解釋,在此解釋下,的每個以D為論域的公式均為真,則稱為可滿足的;如果D的所有解釋都有假公式,則稱是不可滿足的。
不可滿足意義下的一致性
定理1設有謂詞公式G,而其相應的子句集為S,則G是不可滿足的充分必要條件是S是不可滿足的。
要再次強調:公式G與其子句集S並不等值,只是在不可滿足意義下等價。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
當時,若設P的子句集為,的子句集為,則一般情況下,並不等於,而是要比複雜得多。但是,在不可滿足的意義下,子句集與是一致的,即不可滿足不可滿足。
H域上的解釋
定義10如果子句集S的原子集為A,則對A中各元素的真假值的一個具體設定都是S的一個 H解釋。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
可以證明,在給定域D上的任一個解釋,總能在H域上構造一個解釋與之對應,使得如果D域上的解釋能滿足子句集S,則在H域的解釋也能滿足S(即若,就有)。
海伯倫域
海伯倫域
海伯倫域
海伯倫域
海伯倫域
定理2設是子句集S在域D上的一個解釋,則存在對應於的H域解釋,使得若有,就必有。
定理3子句集S不可滿足的充要條件是S對H域上的一切解釋都為假。
證明:充分性:若S在一般域D上是不可滿足的,必然在H域上是不可滿足的,從而對H域上的一切解釋都為假。
海伯倫域
海伯倫域
海伯倫域
必要性:若S在任一H解釋下均為假,必然會使S在D域上的每一個解釋為假。否則,如果存在一個解釋使S為真,那麼依據定理2可知,一定可以在H域找到相對應的一個解釋使S為真。這與S在所有H解釋下均為假矛盾。
定理4子句集S不可滿足的充要條件是存在一個有限的不可滿足的基例集S’。
該常理稱為Herbrand定理。