共找到3條詞條名為merge的結果 展開

merge

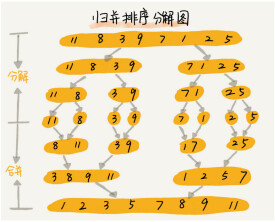
歸併排序演演算法

merge是建立在歸併操作上的一種有效的排序演演算法。它將多個排序列表作為輸入並生成單個列表作為輸出，包含按排序順序排列的輸入列表的所有元素。

目錄
1簡介 2歸併操作 3代碼

簡介

歸併排序是建立在歸併操作上的一種有效的排序演演算法。該演演算法是採用分治法（Divide and Conquer）的一個非常典型的應用。
將已有序的子序列合併，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合併成一個有序表，稱為2-路歸併。

歸併操作

歸併操作(merge)，也叫歸併演演算法，指的是將兩個已經排序的序列合併成一個序列的操作。
如　設有數列{6，202，100，301，38，8，1}
初始狀態： [6] [202] [100] [301] [38] [8] [1] 比較次數
i=1 [6 202 ] [ 100 301] [ 8 38] [ 1 ]　3
i=2 [ 6 100 202 301 ] [ 1 8 38 ]　4
i=3　[ 1 6 8 38 100 202 301 ] 4
總計：　11次代碼

代碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
package sort;
 
import static sort.SortUtils.print;
class MergeSort implements SortAlgorithm {
public > T[] sort(T[] unsorted) {
T[] tmp = (T[]) new Comparable[unsorted.length];
doSort(unsorted, tmp, 0, unsorted.length - 1);
return unsorted;
}
 
private static > void doSort(T[] arr, T[] temp, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
doSort(arr, temp, left, mid);
doSort(arr, temp,mid + 1, right);
merge(arr, temp, left, mid, right);
}
 
}
 
 
private static > void merge(T[] arr, T[] temp, int left, int mid, int right) {
System.arraycopy(arr, left, temp, left, right - left + 1);
int i= left;
int j = mid + 1;
int k = left;
 
while (i <= mid && j <= right) {
if (temp[i].compareTo(temp[j]) <= 0) {
arr[k] = temp[i];
i++;
}
else {
arr[k] = temp[j];
j++;
}
k++;
}
 
while (i <= mid) {
arr[k] = temp[i];
i++;
k++;
}
 
while (j <= right) {
arr[k] = temp[j];
j++;
k++;
}
}
 
public static void main(String[] args) {
// Integer Input
Integer[] arr = {4, 23, 6, 78, 1, 54, 231, 9, 12};
MergeSort mergeSort = new MergeSort();
mergeSort.sort(arr);
 
// Output => 1 4 6 9 12 23 54 78 231
print(arr);
 
// String Inpu
String[] stringArray = {"c", "a", "e", "b","d"};
mergeSort.sort(stringArray);
//Output => a b c d e
print(stringArray);
}
}

基本信息

中文名
歸併排序演算法
外文名
merge
別名
歸併演算法
性質
一種有效的排序演算法