收斂數列
收斂數列
設數列Xn,如果存在常數a,對於任意給定的正數q(無論多小),總存在正整數N,使得n>N時,恆有|Xn-a|Xn收斂於a(極限為a),即數列Xn為收斂數列(Convergent Sequences)。
數列收斂<=>數列存在唯一極限。
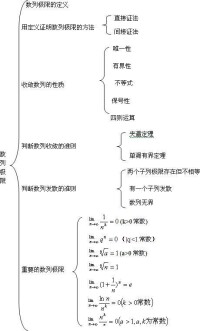
思維導圖
目錄
設數列Xn,如果存在常數a,對於任意給定的正數q(無論多小),總存在正整數N,使得n>N時,恆有|Xn-a|Xn收斂於a(極限為a),即數列Xn為收斂數列(Convergent Sequences)。
數列收斂<=>數列存在唯一極限。

目錄