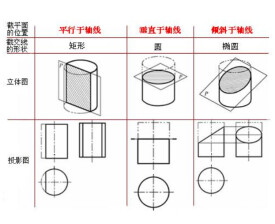
截交線
平面與空間形體表面的交線
截交線是平面與空間形體表面的交線。
當空間形體的表面為平面時,其截交線是多邊形,只須用輔助面法求出多邊形的各頂點即可連成截交線。
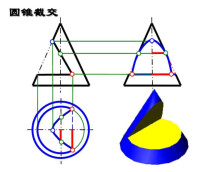
截交線
平面與空間形體表面的交線。它是畫法幾何研究的內容之一。當空間形體表面是曲面時,截交線是一條平面曲線,當空間形體表面由若干個平面組成時,截交線是一個多邊形。在給定平面和空間形體的相對位置后,從多面正投影圖中可以容易地畫出平面和空間形體的投影,但它們截交線的投影一般不能直接畫出,通常需要採用輔助面法先求出截交線上若干點的投影,然後再將它們連接成截交線。
例如圖中圓錐台和空間形體上的斜面相交,須用輔助面法求取截交線上的點。輔助面法是先選取某個面作為輔助面(圖中是水平面),然後作出輔助面和斜面的交線、輔助面和圓錐的交線。圖中這兩條交線分別是直線和圓。最後作出兩交線的交點。所得到的交點就是截交線上的點。改變輔助面的位置,重複上述作圖過程,則能獲得足夠數量的點,連接成截交線。運用輔助面法的關鍵在於選擇合適的輔助面,輔助面和空間形體的交線投影應是直線或者是圓。當空間形體的表面為平面時,其截交線是多邊形,只須用輔助面法求出多邊形的各頂點即可連成截交線。
截交線
截交線的基本性質
(1)共有性。截交線是截平面與立體表面的共有線,截交線上的點也都是它們的共有點。
根據截交線性質,求截交線,就是求出截平面與立體表面的一系列共有點,然後依次連接即可。求截交線的方法,既可利用投影的積聚性直接作圖,也可通過作輔助線的方法求出。
截交線
截交線的形狀
截交線的形狀取決於立體的幾何性質極其與截平面的相對位置,通常為平面折線、平面曲線或平面直線組成。
當平面與片面立體相交時,其截交線為封閉的平面折線。當平面與迴轉提相交時,其截交線一般為封閉的片面曲線或平面曲線和直線圍成的封閉的平面圖或平面多邊形。
畫截交線的一般方法與步驟
求畫截交線就是求畫截平面與立體表面的一系列共有點。求共有點的方法通常有:
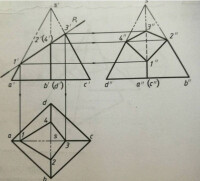
(1)面上取點法:平面與立體相交,截片面處於特殊位置,截交線有一個投影或兩個投影有積聚性,利用積聚性採用面上取點法,求出截交線上共有點的另外一個或兩個投影,此方法稱為面上取點法。下圖所示為一正放的正三稜柱被正垂面P截切,由於截平面P是正垂面,截交線的正面投影可直接確定(即積聚在截平面的有積聚性的同面投影上),截交線的水平投影積聚在正三稜柱各側棱面水平投影上,故由截交線的正面投影和水平投影可求出其側面投影。
(2)線面交點法:平面與立體相交,截平面處於特殊位置,截交線有一個投影或兩個投影有積聚性,求立體表面上的稜線或素線與截平面的交點,該交點即為截交線上的點(共有點),此方法稱為線面交點法。
具體作圖步驟為:
(1)找出屬於截交線上一系列的特殊點;
(2)求出若干一般點;
(3)判別可見性;
(4)順次連接各點(成折線或曲線)。
簡介
工程上常遇到各種各樣的曲面,其中圓錐面佔有特殊且重要的地位。平面截切圓錐形成的截交線—圓、橢圓、雙曲線、拋物線,這些圓錐曲線與人類的生產實踐密切相關,應用範圍比較廣泛。工程上常遇到表面有交線的零件。為了完整、清晰的表達出零件的形狀以便正確的製造零件,應正確的畫出交線。交線通常可分為兩種,一種是平面與立體表面相交形成的截交線。另一種是兩立體表面相交形成的相貫線。
交線是零件上平面與立體表面或兩立體表面的共有線,也是它們表面間的分界線。由於立體由不同表面所包圍,並佔有一定空間範圍,因此,立體表面交線通常是封閉的,如果組成該立體的所有表面,所確定立體的形狀、大小和相對位置已定,則交線也就被確定。
立體的表面交線在一般的情況下是不能直接畫出來的(交線為圓或直線時除外),因此,必須先設法求出屬於交線上的若干點,然後把這些點連接起來。
圓錐截交線及其形狀
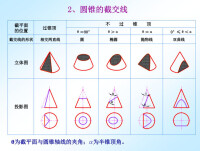
圓錐截交線,顧名思義,即是圓錐與平面相交所產生的一條封閉性平面曲線或由曲線和直線共同圍成的平面圖形。假設圓錐母線和圓錐軸線之間的夾角為 α,(α 為半錐角,一般情況下,對於一個確定的圓錐來說,α 是一個常數),設截平面 P 和圓錐軸線之間的夾角為 θ(θ 的大小範圍是),如下圖 1(d) 中所示。根據截平面 P 與圓錐面兩者的相對位置,可以確定圓錐截交線的形狀有以下 5 種(如下圖 1所示):
①如下圖 1(a) 所示,若截平面 P 恰好過圓錐的頂點,則形成的截交線是圓錐面上的兩條素線。
②如下圖 1(b) 所示,若截平面 P 與圓錐軸線垂直,即 時,所形成的截交線則是一個緯圓。
③如下圖 1(c) 所示,若截平面P斜交於圓錐的軸線,即時,所形成的截交線則是一個拋物線。
④如下圖1(d) 所示,當截平面 P 斜交於圓錐的軸線,且 當時,形成的截交線是一個橢圓。
⑤如下圖 1(e) 所示,當截平面 P 斜交於圓錐的軸線,且 時,所形成的截交線則是一個雙曲線。
應用數學理論論證圓錐截交線的具體形狀
先建立相應的坐標系,假設截平面 P 在 Z 軸上截距為 b,則可以確定圓錐的方程式為,截平面 P 的方程為。則出現以下幾種情況:
(1)若截平面 P 過圓錐的頂點,則此時的,將其代入得: ,且有,即截交線是圓錐面上的兩條素線。
(2)若 截 平 面 垂 直 於 圓 錐 軸線。此 時, 將 其 代 入,結果顯示截交線是一個圓。