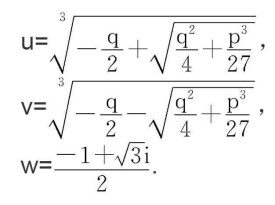卡爾達諾公式
卡爾達諾公式
卡徠爾達諾公式(Cardano formula)亦稱卡丹公式，是三次方程的求解公式，它給出三次方程x+px+q=0的三個解為x1=u+v，x2=uw+vw，x3=uw+vw。由於一般三次方程y+ay+by+c=0經過未知量的代換y=x-a/3后，可化為形如x+px+q=0的三次方程。因此，運用卡爾達諾公式可解任意復係數的三次方程，此公式實為塔爾塔利亞(TN.artaglia)於1541年首先發現，但未公開發表，卻在允諾保密的央求下告訴了卡爾達諾(G.Cardano)，後者於1545年將這一結果發表在自己的著作《大法》里，後人遂稱為卡爾達諾公式，沿襲至今。
卡爾達諾公式是一個著名的求根公式，指實係數一元三次方程
的求根公式，式中
且，此公式也可以應用於復係數三次方程中。
義大利數學家卡爾達諾(G.Cardano)在1545年出版的《大術》一書中，首先發表了上述公式，此公式來自義大利數學家塔爾塔利亞(N.Tartaglia)，但卡爾達諾給出了該公式的幾何證明。
當p，q為實數時，稱為方程(1)的判別式。
當時，方程(1)有三個兩兩不同的實根，稱為不可約情形；
當時，方程(1)有三個實根，當p，q均不為0時，有兩個重根和一個單根；
當時，方程(1)有一個實根與兩個共軛虛根。獲得一元四次方程的根式解法，從而引發了人們對五次以上代數方程的根式解的研究，推動了近世代數學的產生和發展。此外，由於在不可約情形中出現了用虛數表示實根的情形，使人們再次遇到負數開平方，因此促進了對虛數合理性的認識.1572年，義大利數學家邦貝利(Bombelli，R.)在他的《代數》一書中，討論過求解一元三次方程x =15x+4，其三個根為4，卡爾達諾公式表明三次方程有根式解，他的學生費拉里(L.Ferrari)用降階法 。但應用卡爾達諾公式卻是
邦貝利研究后認為，應將負數的平方根像“普通數”那樣運算。後來，德國數學家萊布尼茨(Leibniz，G.W.)也研究過不可約情形，並且深信：用代數方法解此種情形不可能不用到虛數。這使人們逐漸認識到負數開平方有一定的客觀基礎和合理性，加快了人們接受虛數的認識進程。法國數學家韋達(F.Viete)在《論方程的識別與訂正》(完成於1591年，出版於1615年)中，利用三角恆等式給出了不可約情形的方程(1)的根為
式中θ滿足韋達只給出其中一個根。
利用卡爾達諾公式還會出現用無理數表示有理根的情形。例如，方程x -x-6=0有一個根2，但用卡爾達諾公式卻為
因此，在實際求根時，卡爾達諾公式有一定的局限性。
基本信息
- 中文名
- 卡爾達諾公式
- 外文名
- Cardano formula
- 別名
- 卡丹公式
- 所屬學科
- 數學（高等代數）
- 簡介
- 三次方程的求解公式