F分佈
F分佈
F分佈是1924年英國統計學家R.A.Fisher提出,並以其姓氏的第一個字母命名的。F分佈定義為:設X、Y為兩個獨立的隨機變數,X服從自由度為k1的卡方分佈,Y服從自由度為k2的卡方分佈,這2個獨立的卡方分佈被各自的自由度除以後的比率這一統計量的分佈。即:上式F服從第一自由度為k1,第二自由度為k2的F分佈。

F分佈
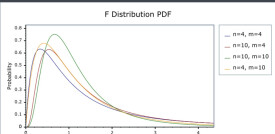
1、它是一種非對稱分佈;
2、它有兩個自由度,即n1 -1和n2-1,相應的分佈記為F( n1 –1, n2-1), n1 –1通常稱為分子自由度, n2-1通常稱為分母自由度;
3、F分佈是一個以自由度
和
為參數的分佈族,不同的自由度決定了F 分佈的形狀。
4、F分佈的倒數性質:
。
性質5:若總體與獨立,為來自X的一個樣本,為來自Y的一個樣本,為已知參數。
性質6:若總體與獨立,為來自X的一個樣本,為來自Y的一個樣本。
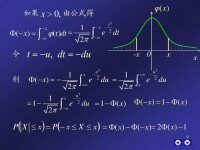
密度函數推導
若總體,與 為來自X的兩個獨立樣本,設統計量
則稱統計量F服從自由度 和 的F分佈。
若總體與總體獨立,為來自X的一個樣本,為來自Y的一個樣本,
則稱統計量F服從自由度為和,非中心參數為的非中心F分佈。