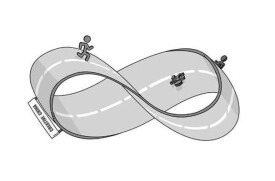
莫比烏斯帶
無窮符號∞
莫比烏斯帶,公元1858年,德國數學家莫比烏斯(Mobius,1790~1868)和約翰·李斯丁發現:把一根紙條扭轉180°后,兩頭再粘接起來做成的紙帶圈,具有魔術般的性質。
普通紙帶具有兩個面(即雙側曲面),一個正面,一個反面,兩個面可以塗成不同的顏色;而這樣的紙帶只有一個面(即單側曲面),一隻小蟲可以爬遍整個曲面而不必跨過它的邊緣。這種紙帶被稱為“莫比烏斯帶”(也就是說,它的曲面從兩個減少到只有一個)。
元,莫烏 ,扭轉粘紙,具魔術般質。普紙具(雙側曲),紙(單側曲),蟲爬遍整曲必跨緣!奇單紙稱“莫烏”(ö ) 。
典型拓撲圖形,莫比烏斯帶引起了許多科學家的研究興趣,並在生活和生產中有了一些應用。例如,動力機械的皮帶就可以做成“莫比烏斯帶”狀,這樣皮帶就不會只磨損一面了。此外,莫比烏斯帶也是藝術家眼中的經典造型 。
科,具展( )莫烏折,盡達具彈量狀態。紀始,莫烏題始終困擾科,即預測維空構。研究,倫敦院非線 組未程,達題 。
莫比烏斯帶本身具有很多奇妙的性質。如果從中間剪開一個莫比烏斯帶,不會得到兩個窄的帶子,而是會形成一個把紙帶的端頭扭轉了兩次再結合的環(並不是梅比斯環),再把剛剛做出那個把紙帶的端頭扭轉了兩次再結合的環從中間剪開,則變成兩個環。如果你把帶子的寬度分為三分,並沿著分割線剪開的話,會得到兩個環,一個是窄一些的莫比烏斯帶,另一個則是一個旋轉了兩次再結合的環。另外一個有趣的特性是將紙帶旋轉多次再粘貼末端而產生的。比如旋轉三個半圈的帶子再剪開後會形成一個三葉結。剪開帶子之後再進行旋轉,然後重新粘貼則會變成數個莫比烏斯帶。
莫比烏斯帶常被認為是無窮大符號“∞”的創意來源,因為如果某個人站在一個巨大的莫比烏斯帶的表面上沿著他能看到的“路”一直走下去,他就永遠不會停下來。但是這是一個不真實的傳聞,因為“∞”的發明比莫比烏斯帶還更要早。
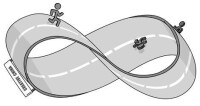
莫比烏斯圈
新得到的這個較長的紙圈,本身卻是一個雙側曲面,它的兩條邊界自身雖不打結,但卻相互套在一起。把上述紙圈,再一次沿中線剪開,這回可真的一分為二了,得到的是兩條互相套著的紙圈,而原先的兩條邊界,則分別包含於兩條紙圈之中,只是每條紙圈本身並不打結罷了。
相反,拿一張白的長紙條,把一面塗成黑色,反方向把其中一端翻一個身,粘成一個莫比烏斯帶。用剪刀沿紙帶的中央把它剪開。紙帶不僅沒有一分為二,反而剪出兩個環套環的莫比烏斯帶。
即;莫比烏斯帶沿著中間剪開,可以得到一個一個兩倍長的紙圈,也可得到兩個環套環的莫比烏斯帶。
莫比烏斯帶還有更為奇異的特性。一些在平面上無法解決的問題,卻不可思議地在莫比烏斯帶上獲得了解決。
比如在普通空間無法實現的"手套易位"問題:人左右兩手的手套雖然極為相像,但卻有著本質的不同。我們不可能把左手的手套貼切地戴到右手上去;也不能把右手的手套貼切地戴到左手上來。無論你怎麼扭來轉去,左手套永遠是左手套,右手套也永遠是右手套!不過,倘若你把它搬到莫比烏斯帶上來,那麼解決起來就易如反掌了。
在自然界有許多物體也類似於手套那樣,它們本身具備完全相像的對稱部分,但一個是左手系的,另一個是右手系的,它們之間有著極大的不同。
製作過程中把紙帶一端旋轉180度可以,旋轉540度、900度……都符合莫比烏斯帶的定義。(在省略號中的數為
180的奇數倍均可以)
可以用參數方程式創造出立體莫比烏斯帶(如右下圖)
這個方程組可以創造一個邊長為1半徑為1的莫比烏斯帶,所處位置為面,中心為。參數
u在v從一個邊移動到另一邊的時候環繞整個帶子。
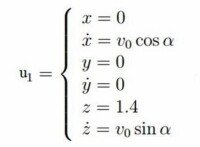
莫比烏斯帶的參數方程
莫比烏斯帶是一個二維的緊緻流形(即一個有邊界的面),可以嵌入到三維或更高維的流形中。它是一個不可定向的的標準範例,可以看作RP#RP。同時也是數學上描繪纖維叢的例子之一。特別地,它是一個有一纖維單位區間,的圓S上的非平凡叢。僅從莫比烏斯帶的邊緣看去給出S上一個非平凡的兩個點(或Z)的從。
莫比烏斯帶是一種拓展圖形,它們在圖形被彎曲、拉大、縮小或任意的變形下保持不變,只要在變形過程中不使原來不同的點重合為同一個點,又不產生新點。換句話說,這種變換的條件是:在原來圖形的點與變換了圖形的點之間存在著一一對應的關係,並且鄰近的點還是鄰近的點。這樣的變換叫做拓撲變換。拓撲有一個形象說法——橡皮幾何學。因為如果圖形都是用橡皮做成的,就能把許多圖形進行拓撲變換。例如一個橡皮圈能變形成一個圓圈或一個方圈。但是一個橡皮圈不能由拓撲變換成為一個阿拉伯數字8。因為不把圈上的兩個點重合在一起,圈就不會變成8,“莫比烏斯帶”正好滿足了上述要求。
傳統的三維世界里,所有的維度都是直線式的,但如果將旋轉視為一種緯度,則相對容易對莫比烏斯帶進行解釋。
兩個旋轉緯度的關係
垂直方向上增加維度的示意
如果垂直方向上旋轉的度數繼續增加,只會增加莫比烏斯帶纏繞的圈數,並不會額外增加空間的維度。
和莫比烏斯帶非常近似的一個幾何學物體叫做克萊因瓶。一個克萊因瓶可以用粘貼兩個莫比烏斯帶的方法製作出來。但是如果物體不進行自我交叉,這個步驟在三維空間內是不可能完成的。
另外一個相近的結構是實射影平面。如果在實射影平面上有一個洞的話,從左側看就會形成一個莫比烏斯帶。或者把莫比烏斯帶的邊界進行有限定義,就會形成一個真投影屏面。更形象地說法是重建莫比烏斯帶的邊緣形成一個普通的環。有一種普遍的誤解認為如果不進行平面的自我交叉就無法在三維空間內形成一個有普通環邊緣的莫比烏斯帶。事實上是可能的,方法是這樣的:定義C為面上的單位圓,現在連接C上面的對跖點,比如θ和。當θ在0到之間運動的時候,在xy面上方做這條線的反餘切,其他情況則在面下做反餘切。
莫比烏斯帶為很多藝術家提供了靈感,比如美術家莫里茨·科內利斯·埃舍爾就是一個利用這個結構在他木刻畫作品裡面的人,最著名的就是莫比烏斯二代,圖畫中表現一些螞蟻在莫比烏斯帶上面前行。
• 它也經常出現在科幻小說裡面,比如亞瑟·克拉克的《黑暗之牆》。科幻小說常常想象我們的宇宙就是一個莫比烏斯帶。由A.J.Deutsch創作的短篇小說《一個叫莫比烏斯的地鐵站》為波士頓地鐵站創造了一個新的行駛線路,整個線路按照莫比烏斯帶方式扭曲,走入這個線路的火車都消失不見。另外一部小說《星際迷航:下一代》中也用到了莫比烏斯帶空間的概念。
• 有一首小詩也描寫了莫比烏斯帶:
• 數學家斷言:莫比烏斯帶只有一邊。如果你不相信,就請剪開一個驗證,帶子分離的時候卻還是相連。
• 莫比烏斯帶也被用於工業製造。一種從莫比烏斯帶得到靈感的傳送帶能使用更長的時間,因為可以更好地利用整個帶子,或者用於製造磁帶,可以承載雙倍的信息量。
• 有一座鋼製的莫比烏斯帶雕塑位於美國華盛頓的史密斯森林歷史和技術博物館。
• 荷蘭建築師Ben Van Berkel以莫比烏斯帶為創作模型設計了著名的莫比烏斯住宅。
• 在日本漫畫《哆啦A夢》中,哆啦A夢有個道具的外觀就是莫比烏斯帶;在故事中,只要將這個環套在門把上,則外面的人進來之後,看到的依然是外面。
• 在電玩遊戲“音速小子-滑板流星故事”中最後一關魔王戰就是在莫比烏斯帶形狀的跑道上進行,如果不打敗魔王,就會一直在莫比烏斯帶上無限循環的跑下去。
• 1988年在日本上映的動畫電影機動戰士高達 逆襲的夏亞以莫比烏斯帶作為對命運的隱喻:人類就好比行走在莫比烏斯帶上的螞蟻一般,永遠逃不出這個怪圈,不斷重複著相同的錯誤,類同的悲劇也在不斷地上演。
• 電影的主題歌BEYOND THE TIME(メビウスの宇宙を越えて)亦呼應了這個主題(日文“メビウス”就是Möbius的意思)。
• jojo奇妙旅程第6部空條徐倫對c-moon一幕亦有於戰鬥中使用此結構。
• 韓國導演金基德2013年的電影《莫比烏斯》命名就取材於莫比烏斯環,象徵人性周而復始的重複悲劇和錯誤。
• 網路上流傳一部動畫影片,用莫比烏斯帶原理,來解釋巴哈所著的逆行卡農作品。
• 《Bilibili拜年祭2017》中作品《再一次》以莫比烏斯帶原理構築了困住木琳與海閱的古堡。