帶分數
假分數的形式之一
帶分數是假分數的另外一種形式。非零整數與真分數相加(負整數時與真分數相減)所成的分數(或真分數與假分數相加減化簡后的分數)。
帶分數是分數的一種形式,通常在正數的範圍內討論。如果在實數部分內討論,絕對值滿足狹義的帶分數定義的,就是廣義的帶分數。帶分數包含兩個部分:整數部分和真分數部分。帶分數和假分數一一對應。
帶分數是假分數的一種形式。非零自然數與真分數相加(負整數時與真分數相減)所成的分數(或真分數與假分數相加減化簡后的數),一般讀作幾又幾分之幾,假分數的倒數一定不大於一。
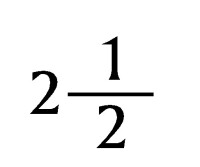
帶分數
如果在實數部分內討論,絕對值滿足狹義的帶分數定義的,就是廣義的帶分數。
帶分數包含兩個部分:整數部分和真分數部分。
帶分數和假分數一一對應。
整數部分
帶分數的整數部分不得為零。
分數部分
帶分數的分數部分,必須是真分數。即分子的絕對值必須小於分母的絕對值。
帶分數=整數+真分數
註:整數部分不等於0
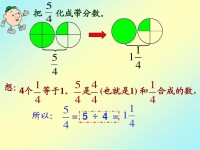
這是一個典型的帶分數
注意:
1.帶分數的分數部分不能是假分數。
2.帶分數與字母相乘時要寫成假分數的形式。
在代數學中,通常不用帶分數,只用假分數。所以,帶分數變得比較少見。
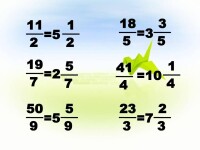
帶分數
計算帶分數加減法,要把整數部分與分數部分分別相加減。如果被減數的分數部分小於減數的分數部分,需要從被減數的整數部分拿出1化成假分數,和原來被減數的分數部分合併起來再減。
帶分數計算乘除法時,需要化成假分數來計算。
把假分數化成整數或帶分數,要用分子除以分母:
能整除的,所得的商就是整數;
不能整除的,商就是帶分數的整數部分,餘數就是分數部分的分子,分母不變。
