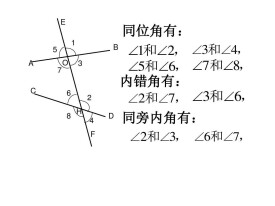
同位角

同位角的特徵識別：

1.在截線的同旁；

2.在被截兩直線的同方向；

3同位角通常是成對出現的。

小竅門：平面內的n（n大於等於3）條直線相交，可得同位角最少有2(n-1)(n-2)對。

平行線的性質：兩直線平行，同位角相等。

兩直線平行，內錯角相等。

兩直線平行，同旁內角互補

平行線的判定：同位角相等，兩直線平行。

內錯角相等，兩直線平行。

同旁內角互補，兩直線平行。

（1）如圖，有多少對同位角？

答案：有4對。∠4與∠5，∠3與∠6，∠1與∠8，∠2與∠7均為同位角。

（2）判斷：同一平面內，兩直線被第三條直線截斷所得的同位角相等。

（錯）理由：只有在兩直線平行的前提下，同位角才相等。

同位角、內錯角、同旁內角是在兩條直線被第三條直線所截時形成的，(常說成三線八角)。

1、同位角的特徵。如圖，∠1_與∠5為同位角。分析它們的特點：都在兩條直線a、b的上方，且都在截線c的右側。由此得到同位角特徵：兩條直線被第三條直線所截時，都在兩條直線的同一方向，且在截線的同側的兩個角互為同位角。如圖中∠4與∠6，∠2與∠8，∠3與∠7具有此特點。

2、內錯角的特徵。如圖，∠2與∠6為內錯角，分析它們的特點：夾在兩條直線a、b的內部，且在截線c的左右兩側，由此得到內錯角的特徵：兩條直線被第三條直線所截時，夾在兩條直線的內部，且在截線兩側的兩個角互為內錯角。如圖1中：∠3與∠5具有此特點，也是一對內錯角。

3、同旁內角的特徵。如圖，∠2與∠5為同旁內角，分析它們的特點：夾在直線a、b的內部，且在截線c的同一側。由此得到同旁內角的特徵：兩條直線被第三條直線所截時，夾在兩條直線的內部，且在截線同側的兩個角互為同旁內角。如圖中：∠3與∠6有此特點，是一對同旁內角。