共找到2條詞條名為笛卡爾乘積的結果 展開
- 數學幾何概念
- 直積
笛卡爾乘積
數學幾何概念
在數學中，兩個集合X和Y的笛卡兒積（Cartesian product），又稱直積，表示為X × Y，第一個對象是X的成員而第二個對象是Y的所有可能有序對的其中一個成員。假設集合A=a, b，集合B=0, 1, 2，則兩個集合的笛卡爾積為(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)。類似的例子有，如果A表示某學校學生的集合，B表示該學校所有課程的集合，則A與B的笛卡爾積表示所有可能的選課情況。A表示所有聲母的集合，B表示所有韻母的集合，那麼A和B的笛卡爾積就為所有可能的漢字全拼。
笛卡爾1596年3月31日生於法國土倫省萊耳市的一個貴族之家，笛卡爾的父親是布列塔尼地方議會的議員，同時也是地方法院的法官，笛卡爾在豪華的生活中無憂無慮地度過了童年。
笛卡爾1612年到普瓦捷大學攻讀法學，四年後獲博士學位。1616年笛卡爾結束學業后，便背離家庭的職業傳統，開始探索人生之路。他投筆從戎，想藉機遊歷歐洲，開闊眼界。
在荷蘭長達20多年的時間裡，笛卡爾對哲學、數學、天文學、物理學、化學和生理學等領域進行了深入的研究，並通過數學家梅森神父與歐洲主要學者保持密切聯繫。他的主要著作幾乎都是在荷蘭完成的 。
1628年，笛卡爾寫出《指導哲理之原則》，1634年完成了以哥白尼學說為基礎的《論世界》。書中總結了他在哲學、數學和許多自然科學問題上的一些看法。1637年，笛卡爾用法文寫成三篇論文《折光學》、《氣象學》和《幾何學》，並為此寫了一篇序言《科學中正確運用理性和追求真理的方法論》，哲學史上簡稱為《方法論》，6月8日在萊頓匿名出版。1641年出版了《形而上學的沉思》，1644年又出版了《哲學原理》等重要著作。
1649年冬，笛卡爾應瑞典女王克里斯蒂安的邀請，來到了斯德哥爾摩，任宮廷哲學家，為瑞典女王授課。由於他身體孱弱，不能適應那裡的氣候，1650年初便患肺炎抱病不起，同年二月病逝。終年54歲。1799年法國大革命后，笛卡爾的骨灰被送到了法國歷史博物館 。
設A,B為集合，用A中元素為第一元素，B中元素為第二元素構成有序對，所有這樣的有序對組成的集合叫做A與B的笛卡爾積，記作AxB.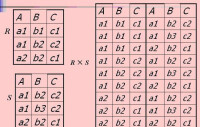
笛卡爾乘積
笛卡爾積的符號化為：
A×B={(x,y)|x∈A∧y∈B}
例如，A={a,b}, B={0,1,2}，則
A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}
1.對任意集合A，根據定義有
AxΦ =Φ ，Φ xA=Φ
2.一般地說，笛卡爾積運算不滿足交換律，即
AxB≠BxA（當A≠Φ ∧B≠Φ∧A≠B時）
3.笛卡爾積運算不滿足結合律，即
（AxB)xC≠Ax(BxC）（當A≠Φ ∧B≠Φ∧C≠Φ時)
4.笛卡爾積運算對並和交運算滿足分配律，即
Ax(B∪C)=(AxB）∪（AxC)
(B∪C)xA=(BxA）∪（CxA)
Ax(B∩C)=(AxB）∩（AxC)
(B∩C)xA=(BxA）∩（CxA)
給出三個域：
D1=SUPERVISOR ={ 張清玫，劉逸 }
D2=SPECIALITY={計算機專業，信息專業}
D3=POSTGRADUATE={李勇，劉晨，王敏}
則D1，D2，D3的笛卡爾積為D：
D=D1×D2×D3 =
{（張清玫，計算機專業，李勇），（張清玫，計算機專業，劉晨），
（張清玫，計算機專業，王敏），（張清玫，信息專業，李勇），
（張清玫，信息專業，劉晨），（張清玫，信息專業，王敏），
（劉逸，計算機專業，李勇），（劉逸，計算機專業，劉晨），
（劉逸，計算機專業，王敏），（劉逸，信息專業，李勇），
（劉逸，信息專業，劉晨），（劉逸，信息專業，王敏） }
這樣就把D1,D2,D3這三個集合中的每個元素加以對應組合，形成龐大的集合群。
本個例子中的D中就會有2X2X3個元素，如果一個集合有1000個元素，有這樣3個集合，他們的笛卡爾積所組成的新集合會達到十億個元素。假若某個集合是無限集，那麼新的集合就將是有無限個元素。
C#源代碼
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;
using System.Linq;
public class Descartes
{
public static void run(List> dimvalue, List result, int layer, string curstring)
{
if (layer < dimvalue.Count - 1)
{
if (dimvalue[layer].Count == 0)
run(dimvalue, result, layer + 1, curstring);
else
{
for (int i = 0; i < dimvalue[layer].Count; i++)
{
StringBuilder s1 = new StringBuilder();
s1.Append(curstring);
s1.Append(dimvalue[layer][i]);
run(dimvalue, result, layer + 1, s1.ToString());
}
}
}
else if (layer == dimvalue.Count - 1)
{
if (dimvalue[layer].Count == 0) result.Add(curstring);
else
{
for (int i = 0; i < dimvalue[layer].Count; i++)
{
result.Add(curstring + dimvalue[layer][i]);
}
}
}
}
}
程序使用說明
（1）將每個維度的集合的元素視為List,多個集合構成List> dimvalue作為輸入
（2）將多維笛卡爾乘積的結果放到List result之中作為輸出
（3）int layer, string curstring只是兩個中間過程的參數攜帶變數
（4）程序採用遞歸調用，起始調用示例如下：
List result = new List();
Descartes.run(dimvalue, result, 0, "");
即可獲得多維笛卡爾乘積的結果。
基本信息
- 中文名
- 笛卡爾乘積
- 外文名
- Cartesian product
- 應用學科
- 數學
- 適用領域
- 運算
- 別名
- 直積
- 表達式
- A×B = {(x,y)|x∈A∧y∈B}
- 提出者
- 笛卡爾