子格

子格

子格(sublattice)是格論的基本概念之一，設(L，∨，∧)是一格，T是L的非空子集，如果T關於兩種運算都是封閉的，則稱(T，∨，∧)是(L，∨，∧)的子格。顯然，子格本身是一個格。

目錄

1基本介紹 2例題解析

基本介紹

設S是格L的子集，若S關於L中的二元運算∧和∨是封閉的，即對任意a，，，，則稱S為L的子格；若子格S含0，1，則稱S為格L的{0，1}-子格，若a，，，則是L的子格，稱為閉區間，同樣可定義半開區間(a，b]和[a，b)以及開區間(a，b)，設H為格L的非空子集，L中一切包含H的子格的交，稱為L的由H生成的子格，記為[H]；稱H為[H]的一個生成系，設S是格L的子格，若除L外，沒有真包含S的子格，則稱S為L的極大子格，格L的一切極大子格的交集稱為弗拉梯尼子格，格L的所有子格按集合的包含關係構成格，記為Sub(L)。

例如對構成一格。其哈斯圖如圖1所示。而

，

，

，

，

，

，

，

，

等都是的子格，其中B，B為其平凡子格。有興趣的讀者可以自己求一求共有多少個不同的子格。

例題解析

【例1】D表示90的全體因子的集合，包括1和90，D上整除|關係構成格。

(1)畫出格的哈斯圖。

(2)計算，，和。

(3)求D的所有含4個元素且包含1和90的子格。

解 (1)格(D，|)所對應的哈斯圖如圖2所示。

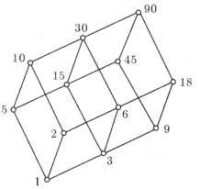
圖2

(2)從圖中可以看出：

，，，．

(3)通過對除去1，90之後的10個元素的二元素組合共=45個進行驗證，可求出滿足條件的子格共24個，有：

{1，2，6，90}，{1，2，10，90}，{1，2，18，90}，{1，2，30，90}，

{1，2，45，90}，{1，3，6，90}，{1，3，9，90}，{1，3，15，90}，

{1，3，18，90}，{1，3，30，90}，{1，3，45，90}，{1，5，10，90}，

{1，5，15，90}，{1，5，18，90}，{1，5，30，90}，{1，5，45，90}，

{1，6，18，90}，{1，6，30，90}，{1，9，10，90}，{1，9，18，90}，

{1，9，45，90}，{1，10，30，90}，{1，15，30，90}，{1，1 5，45，90}.

說明對子格的求法，沒有統一標準的方法，此題只需通過窮舉所有的可能即可。

目錄