內切圓

幾何學術語

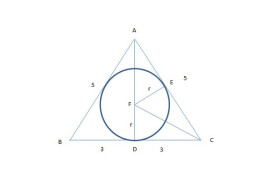
與多邊形各邊都相切的圓叫做多邊形的內切圓。特殊地，與三角形三邊都相切的圓叫做三角形的內切圓，圓心叫做三角形的內心，三角形叫做圓的外切三角形。三角形的內心是三角形三條角平分線的交點。

三角形一定有內切圓，其他的圖形不一定有內切圓，且內切圓圓心定在三角形內部。

目錄

1定義 2性質 3計算

定義

在數學中，若一個二維平面上的多邊形的每條邊都能與其內部的一個圓形相切，該圓就是多邊形的內切圓，這時稱這個多邊形為圓外切多邊形。它亦是多邊形內部最大的圓形。內切圓的圓心被稱為該多邊形的內心。

一個多邊形至多有一個內切圓，也就是說對於一個多邊形，它的內切圓，如果存在的話，是唯一的。並非所有的多邊形都有內切圓。三角形和正多邊形一定有內切圓。擁有內切圓的四邊形被稱為圓外切四邊形。

性質

（1）在三角形中，三個角的角平分線的交點是內切圓的圓心，圓心到三角形各個邊的垂線段相等。

（2）正多邊形必然有內切圓，而且其內切圓的圓心和外接圓的圓心重合，都在正多邊形的中心。

（3）常見輔助線：過圓心作垂直。

計算

1)對於一般的三角形，三角形面積公式如下：

s=r（a+b+c）/2

2)在直角三角形s=r(a+b+c)/2的內切圓中，有這樣兩個簡便公式如下

● 兩直角邊相加的和減去斜邊后除以2，得數是內切圓的半徑：

r=(a+b-c)/2（註：s是Rt△的面積，a, b是Rt△的2個直角邊，c是斜邊）

● 兩直角邊乘積除以直角三角形周長，得數是內切圓的半徑：

r=ab/ (a+b+c)

補充

扇形內切圓

與扇形⌒AOB的圓弧⌒AB及兩條半徑OA,OB都相切的圓叫扇形的內切圓。

內切圓圓心O′在扇形的圓心角AOB的角平分線上

OO′=R-r(R是扇形半徑,r是內切圓半徑)

過O′作O′A⊥OA,垂足A,直角三角形OAO′中

∠O′OA=30°,O′A=r,OO′=R-r

∴r=(R-r)*sin30°,r=1/2(R-r),R=3r

內切圓面積=πr^2

扇形面積是原來圓面積的60/360=1/6

∴扇形面積=πR^2/6=π(3r)^2/6=3πr^2/2

∴扇形的內切圓面積與扇形面積的比為πr^2:(3πr^2/2)=2:3

直角三角形的內切圓的半徑=二分之一×（直角邊+另一直角邊－斜邊）

內切圓的半徑為r=2S÷C，當中S表示三角形的面積，C表示三角形的周長。

內切圓等於外切圓的2分之1

面積與原正方形比為π：4

目錄