中序遍歷
應用於計算機科學學科的遍歷
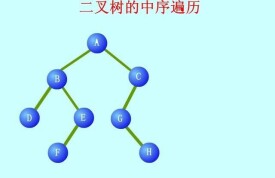
中序遍歷(LDR)是二叉樹遍歷的一種,也叫做中根遍歷、中序周遊。在二叉樹中,中序遍歷首先遍歷左子樹,然後訪問根結點,最後遍歷右子樹。
序遍歷首遍歷左樹,訪根,遍歷右樹。若二叉樹空則束返,否則:
()序遍歷左樹
()訪根
(3)中序遍歷右子樹
如右圖所示二叉樹,中序遍歷結果:DBEAFC
當對一棵數學表達式樹進行中序,前序和後序遍歷時,就分別得到表達式的中綴、前綴和後綴形式。中綴(infix)形式即平時所書寫的數學表達式形式,在這種形式中,每個二元操作符(也就是有兩個操作數的操作符)出現在左操作數之後,右操作數之前。在使用中綴形式時,可能會產生一些歧義。例如,x+y ×z可以理解為(x+y) ×z或x+ (y ×z)。為了避免這種歧義,可對操作符賦於優先順序並採用優先順序規則來分析中綴表達式。在完全括弧化的中綴表達式中,每個操作符和相應的操作數都用一對括弧括起來。更甚者把操作符的每個操作數也都用一對括弧括起來。如( (x) + (y) ),( (x) + ( (y) * (z) ) )和( ( (x) + (y) ) * ( (y) + (z) ) ) * (w)。
設二叉樹中元素數目為n,中序遍歷演演算法的空間複雜性均為O (n),時間複雜性為(n)。
當t的高度為n時(右斜二叉樹的情況),通過觀察其前序、中序和後序遍歷時所使用的遞歸棧空間即可得到上述結論。
c++版本
樹中節點結構為:

樹中節點結構
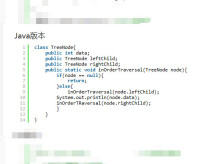
Java版本
C#版本

C#版本
核心代碼:
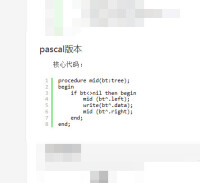
pascal版本