幾何作圖

1.已知— 敘述所給的作圖條件。

2.求作—說明要求作出合乎題設條件的圖形。

3.分析—繪製草圖，根據已知條件分析，找出作圖方法，定出符合條件的圖形。

4.作法—敘述作圖過程和方法，畫出所求圖形。

5.證明—求證所作圖形的正確性。

6.討論—根據題設條件，討論所作圖形在什麼情況下是唯一解、多解、無解、不定解。

以上作圖步驟屬於一般情況，如命題比較簡單，可省略某些步驟。

以下是一個具體例子。

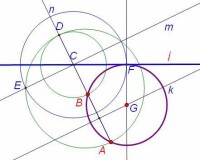
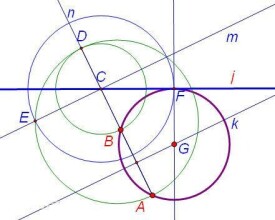
過兩定點作圓與定線相切。已知：定點A、B，定線j 。

求作：過A、B點且與線j相切的圓。

分析：

1、所求圓的圓心必在AB的垂直平分線上。

2、根據圓的切割線定理（切線長度是割線長度的比例中項）可定出所求圓在定線上的切點。

作法：

1、過A、B作射線n交線j於C。

2、作線段AB的垂直平分線k。

3、過C點作線k的平行線m。

4、以C點為圓心CB長為半徑作圓交射線n於D。

5、以AD長為直徑作圓交線m於E。

6、以C點為圓心CE長為半徑作圓交定線j於F。

7、過F點作定線j垂線交線k於G。

8、以G為圓心GF長為半徑作圓，必通過A、B點且與定線j相切。

證明：略。

討論：

1、由於作法6、中交線j的點有2個，即滿足條件的切點有2點，所以本作圖題有2解。

2、由於篇幅關係，本題作法和作圖僅寫出一解。

1.化圓為方－求作一正方形使其面積等於一已知圓；

2.三等分任意角；

3.倍立方－求作一立方體使其體積是一已知立方體的二倍。

圓與正方形都是常見的幾何圖形，但如何作一個正方形和已知圓等面積呢？若已知圓的半徑為1則其面積為π(1)2=π，所以化圓為方的問題等於去求一正方形其面積為π，也就是用尺規做出長度為π1/2的線段（或者是π的線段）。

三大問題的第二個是三等分一個角的問題。對於某些角如90。、180。三等分並不難，但是否所有角都可以三等分呢？例如60。，若能三等分則可以做出20。的角，那麼正18邊形及正九邊形也都可以做出來了（註：圓內接一正十八邊形每一邊所對的圓周角為360。/18=20。)。其實三等分角的問題是由求作正多邊形這一類問題所引起來的。

第三個問題是倍立方。埃拉托塞尼（公元前276年~公元前195年）曾經記述一個神話提到說有一個先知者得到神諭必須將立方形的祭壇的體積加倍，有人主張將每邊長加倍，但我們都知道那是錯誤的，因為體積已經變成原來的8倍。這些問題困擾數學家一千多年都不得其解，而實際上這三大問題都不可能用直尺圓規經有限步驟可解決的。

1637年笛卡兒創建解析幾何以後，許多幾何問題都可以轉化為代數問題來研究。1837年旺策爾(Wantzel)給出三等分任一角及倍立方不可能用尺規作圖的證明。1882年林得曼（Linderman）也證明了π的超越性（即π不為任何整數係數多次式的根），化圓為方的不可能性也得以確立。