馬鞍面
馬鞍面
馬鞍面，是一種曲面，又叫雙曲拋物面，形狀類似於馬鞍。在XOZ坐標平面上構造一條開口向上的拋物線，然後在YOZ坐標平面上構造一條開口向下的拋物線（兩條拋物線的頂端是重合於一點上）；然後讓第一條拋物線順著另一條拋物線上滑動，便形成了馬鞍面。坐標原點為馬鞍面的鞍點。
目錄
定義
函數解析式為:z=xy(定義在xoy平面)
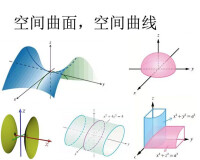
馬鞍面
設one=1,two=4,three=1,four=10;
f(x)=one/two*x^2（開口向上的拋物線）
g(y)=-three/four*y^2（開口向下的拋物線）
z=f(x)-g(y)（主函數）
在幾何畫板5中效果如下：
（軟體的原因，馬鞍的背面顯示不出來，所以只能看到上面）
雙曲拋物面，也叫馬鞍面。其方程為x^2/a^2-y^2/b^2=2z.所謂雙曲，是說不論沿平行於xoz面切還是沿yo平行於z面切都會得到拋物面
基本信息
- 中文名
- 馬鞍面
- 類型
- 雙曲拋物面
- 外文名
- Saddle surface
- 形狀
- 馬鞍
- 函數解析式
- z=x2/a2-y2/b2(定義在xoy平面)
- 長相
- 形近於雙曲面，馬鞍的形狀