矢量運算
一種運算方式
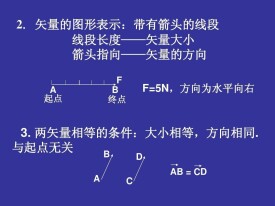
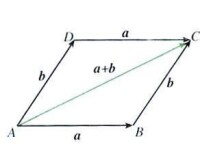
矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的逆運算,一個矢量減去另一個矢量,等於加上那個矢量的負矢量。A-B=A+(-B)。
矢量運算
3D engine中用到的矢量運算詳細內容:
一、兩點距離
2D系統:
Point1(x1,y1),Point2(x2,y2)
距離D=sqr((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2))
3D系統:
Point 1 (x1, y1, z1) Point 2 at (x2, y2, z2).
xd = x2-x1
yd = y2-y1
zd = z2-z1
距離Distance = SquareRoot(xd*xd + yd*yd + zd*zd)
做遊戲和demo永遠不要去做開方:
1、用LUT查表技術Look up Table
2、在做碰撞檢測時,誤差Distance*Distance
二規格化,單位化(Normalize)
先要說矢量的長度:
矢量Vector(x,y,z)
矢量長度Length(Vector)= |Vector|=sqr(x*x+y*y+z*z)
Normalize后:
(x/Length(Vector),y/Length(Vector),z/Length(Vector))
矢量運算
三。點乘 點積 數量積(Dot Product)
是一回事兒。首先明確兩個矢量的點積是個標量.
中學物理的力做功就是矢量點積的例子:W=|F|.|S|.cos(theta)
二矢量點積:
Vector1:(x1,y1,z1) Vector2(x2,y2,z2)
DotProduct=x1*x2+y1*y2+z1*z2
很重要的應用:
1、求二矢量餘弦:
由我們最熟悉的力做功:
cos(theta)=F.S/(|F|.|S|)
可以判斷二矢量的方向情況: cos=1同向,cos=-1相反,cos=0直角
曲面消隱(Cull face)時判斷物體表面是否可見:(法線和視線矢量的方向問題)cos>0不可見,cos<0可見
OpenGL就是這麼做的。
2、Lambert定理求光照強度也用點積:
Light=K.I.cos(theta)
K,I為常數,theta是平面法線與入射光線夾角
老王頭的Fast Bump(Add Hyper Link here)也就是依據這個數學模型。但是他用了個很Cheap的Hack來模擬cosine
四、叉乘(Cross product)
叉乘:Vector1(x1,y1,z1),Vector2(x2,y2,z2):
其結果是個矢量。
方向是Vector1,Vector2構成的平面法線。再使用右手定則
長度是Length(Vector1)*Length(Vector2)*sin(theta)
theta是Vector1 & Vector2的夾角.
所以,平行的矢量叉乘結果為0矢量(長為0,方向任意)
計算結果矢量:(ox,oy,oz)
ox = (y1 * z2) - (y2 * z1)
oy = (z1 * x2) - (z2 * x1)
oz = (x1 * y2) - (x2 * y1)
用途:計演演算法向量,這是生成3D圖形的很關鍵一步。