函數依賴

設R(U)是一個屬性集U上的關係模式，X和Y是U的子集。

若對於R(U)的任意兩個可能的關係r1、r2，若r1[x]=r2[x],則r1[y]=r2[y]，或者若r1[y]不等於r2[y],則r1[x]不等於r2[x]，稱X決定Y，或者Y依賴X。

上面一段話是某些教材上的話，比較不好理解。比如在設計學生表時，一個學生的學號能決定學生的姓名，也可稱姓名屬性依賴於學號，對於現實來說，就是如果知道一個學生的學號，就一定能知道學生的姓名，這種情況就是姓名依賴於學號，這就是函數依賴，函數依賴又分為非平凡依賴，平凡依賴；從性質上還可以分為完全函數依賴、部分函數依賴和傳遞函數依賴。

Y=f(x)

1.數據依賴

在計算機科學中，數據依賴是指一種狀態，當程序結構導致數據引用之前處理過的數據時的狀態。其中最重要的是函數依賴和多值依賴。

2.函數依賴

設X,Y是關係R的兩個屬性集合，當任何時刻R中的任意兩個元組中的X屬性值相同時，則它們的Y屬性值也相同，則稱X函數決定Y，或Y函數依賴於X。

3.平凡函數依賴

當關係中屬性集合Y是屬性集合X的子集時(Y⊆X)，存在函數依賴X→Y，即一組屬性函數決定它的所有子集，這種函數依賴稱為平凡函數依賴。

4.非平凡函數依賴

當關係中屬性集合Y不是屬性集合X的子集時，存在函數依賴X→Y，則稱這種函數依賴為非平凡函數依賴。

5.完全函數依賴

設X,Y是關係R的兩個屬性集合，X’是X的真子集，存在X→Y，但對每一個X’都有X’!→Y，則稱Y完全函數依賴於X。

6.部分函數依賴

設X,Y是關係R的兩個屬性集合，存在X→Y，若X’是X的真子集，存在X’→Y，則稱Y部分函數依賴於X。

7.傳遞函數依賴

設X,Y,Z是關係R中互不相同的屬性集合，存在X→Y(Y!→X),Y→Z，則稱Z傳遞函數依賴於X。

1.函數依賴不是指關係模式R的某個或某些關係實例滿足的約束條件，而是指R的所有關係實例均要滿足的約束條件。

2.函數依賴是語義範疇的概念。只能根據數據的語義來確定函數依賴。

例如“姓名→年齡”這個函數依賴只有在不允許有同名人的條件下成立

3.資料庫設計者可以對現實世界作強制的規定。例如規定不允許同名人出現，函數依賴“姓名→年齡”成立。所插入的元組必須滿足規定的函數依賴，若發現有同名人存在，則拒絕裝入該元組。

屬性之間有三種關係，但並不是每一種關係都存在函數依賴。設R(U)是屬性集U上的關係模式，X、Y是U的子集：

●如果X和Y之間是1：1關係（一對一關係），如學校和校長之間就是1:1關係，則存在函數依賴X→Y和Y→X。

●如果X和Y之間是1：n關係（一對多關係），如年齡和姓名之間就是1:n關係，則存在函數依賴Y→X。

●如果X和Y之間是m：n關係（多對多關係），如學生和課程之間就是m:n關係，則X和Y之間不存在函數依賴。

例:Student(Sno,Sname,Ssex,Sage,Sdept)

假設不允許重名，則有:

Sno→Ssex，Sno→Sage,Sno→Sdept，

Sno←→Sname,Sname→Ssex，Sname→Sage

Sname→Sdept

但Ssex－\→Sage

若X→Y，並且Y→X,則記為X←→Y。

若Y不函數依賴於X,則記為X－\→Y。

在關係模式R(U)中，對於U的子集X和Y，

1.如果X→Y，但Y不為X的子集，則稱X→Y是非平凡的函數依賴

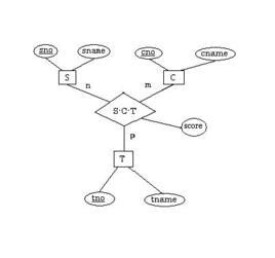
例：在關係SC(Sno,Cno,Grade)中，

非平凡函數依賴：(Sno,Cno)→Grade。

2.若X→Y，但Y為X的子集，則稱X→Y是平凡的函數依賴

平凡函數依賴：(Sno,Cno)→Sno，(Sno,Cno)→Cno。

3.若x→y並且，存在x的真子集x1，使得x1→y,則y部分依賴於x。

例：學生表（學號，姓名，性別，班級，年齡）關係中，

部分函數依賴：（學號，姓名）→性別，學號→性別，所以（學號，姓名）→性別是部分函數依賴。

4.若x→y並且，對於x的任何一個真子集x1，都不存在x1→y則稱y完全依賴於x。

例：成績表（學號，課程號，成績）關係中，

完全函數依賴：（學號，課程號）→成績，學號－\→成績，課程號－\→成績，所以（學號，課程號）→成績是完全函數依賴。

5.若x→y並且y→z，而y－\→x，則有x→z，稱這種函數依賴為傳遞函數依賴。

例：關係S1（學號，系名，系主任），

學號→系名，系名→系主任，並且系名－\→學號，系主任－\→系名，所以學號→系主任為傳遞函數依賴。