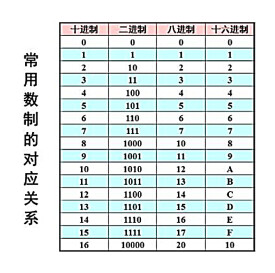
二十四進位

最初的計時法是六十進位，即每60小單位進1大單位的進位，也就是我們所說的1小時=60分鐘，1分鐘=60秒。這是因為60是一個奇妙的數，它可以被1,2,3,4,5,6,10,12,15,20,30,60整除，所以用來計時十分方便。後來西方人把60除以10再乘2，得到12，並規定午夜為0時，正午為12時（am）；正午為0時，午夜為12時（pm）。中國人把一天12等分，每一份稱為一個時辰，並用地支編號。一個時辰等於兩個小時。中國人規定晚上11時至次日凌晨1時為子時（三更），中午11時至1時為午時。最後，因為西方時間後面加am和pm的不簡便性和中國時辰的不通用性，在正式表達時間時確定用二十四小時制。

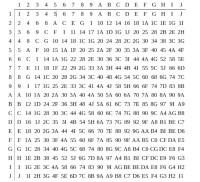
在中國近代化的過程中，中國人已經完全適應西方的十二進位，突然改成二十四進位未免會不適應。西方人用了那麼久的十二進位會更不適應。美國人民直到現在都普遍不適應。而且在指針式鐘錶中，時間也是十二進位的，所以中國人表達大於等於13時的時間就會將時間減去12再表達。美國人普遍看不懂二十四小時制。

二十四進位的優點在於不需要添加輔助符號（am和pm）就可以完整地表達時間，被廣泛應用於大型公共交通（軌道交通、輪船、客機）和軍事。

二十四進位有24個基數：0、1、2、3、4、5、6、7、8、9、A（10）、B（11）、C（12）、D（13）、E（14）、F（15）、G（16）、H（17）、J（18）、K（19）、L（20）、M（21）、N（22）、P（23）（A~~P代表10~~23）。為了避免混淆1和I，0和O，故跳過字母I、O，18~~23分別計作J、K、L、M、N、P。比如：16計作G、22計作N。等於或大於24的數字計作：24→10、25→11、26→12……25→11中標粗體的1代表24。同一個數字在不同的位置代表的值是不一樣的。

例：1→24、10→24、100→24、1000→24、10000→24……

如果有一位的數字不是1，就用1的值乘相應數值。注意：A~~P代表10~~23，具體代表的數值見上文。

例：2D→2×24+13（D）×24=48+13=61

如果計作分數，那麼1/2→0.C、1/3→0.8、2/3→0.G、1/4→0.6、3/4→0.J……

逢24進1，意思是：每一位上的數大於24，就向前一位進1（那一位上的數減的是24，不是全減）或先轉十進位。

例：36+4J=

解：36→3×24+6×24→72+6=78

4J→4×24+18（J）×24→96+18=114

78+114=192

192→80

或者列豎式：

答：36+4J=80

如果有一位上的數字不夠減，向前一位借1當24來用。

例：7J-4P=

解：4P→4×24+23（P）×24→96+23=119

7J→7×24+18（J）×24→168+18=186

186-119=67

67→2K

或者列豎式：

答：7J-4P=2K

方法一：

把乘法分解成加法就行了。如：

例：43×A=

解：43×A=43+43+43+43+43+43+43+43+43+43=1H6

答：43×A=1H6

方法二：乘法直接運算

3×A→3×10=30→16

4×A+1→4×10+1=41→1H

答：43×A=1H6

有一種記數系統便是24進位的，其中1~24有專門的符號來表示，大於24的數便可以像24進位那樣寫成多位數，如tokaputokapuŋgayepoko代表24進位中的P0（552）。malapu talusupuŋga talu代表24進位中的H2G（9856）。