共找到2條詞條名為置換的結果展開

置換

置換的廣義概念在不同語境下有不同的形式定義：

在集合論中，一個集合的置換是從該集合映至自身的雙射；在有限集的情況，便與上述定義一致。

在組合數學中，置換一詞的傳統意義是一個有序序列，其中元素不重複，但可能有闕漏。例如1,2,4,3可以稱為1,2,3,4,5,6的一個置換，但是其中不含5,6。此時通常會標明為“從n個對象取r個對象的置換”。

在集合論與抽象代數等領域中，“置換”一詞被保留為集合（通常是有限集）到自身的雙射的一個稱呼。例如對於從一到十的數字構成的集合，其置換將是從集合到自身的雙射。一個集合上的置換在函數合成運算下構成一個群，稱為對稱群或置換群。

由於元素的有限集可以一一對應到集合，有限集的置換可以化約到形如 {1, ..., n} 的集合之置換。此時有兩種表示法。

第一，利用矩陣符號將自然排序寫在第一列，而將置換后的排序寫在第二列。

第二，藉由置換的相繼作用描述，這被稱為“輪換分解”。

長度等於二的輪換稱為換位，這種輪換是將元素交換，並保持其它元素不變。對稱群可以由換位生成。

輪換長度為偶數的輪換稱為偶輪換，反之則為奇輪換；由此可定義任一置換的奇偶性，並可證明：一個置換是偶置換的充要條件是它可以由偶數個換位生成。偶輪換在置換群中構成一個正規子群，稱為交錯群。

在計算機學科中，賦值/代入的差別表明函數式編程與指令式編程之差異。純粹的函數式編程並不提供賦值機制。現今數學的慣例是將置換看作函數，其間運算看作函數合成，函數式編程也類似。就賦值語言的觀點，一個代入是將給定的值“同時”重排，這是個有名的問題。

(2,5,1,4,3,6)的置換圖取一個無向圖G，將圖G的n個頂點標記v1,...,vn，對應一個置換( s(1) s(2) ... s(n) )，當且僅當s(i) < s(j) 而i>j，則圖的vi和vj相連，這樣的圖稱為置換圖。

置換圖的補圖必是置換圖。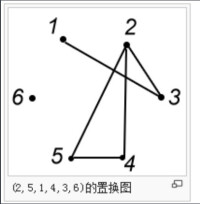

置換

多數計算機都有個計算置換數的nPr鍵。然而此鍵在一些最先進的桌上型機種中卻被隱藏了。例如：在 TI-83 中，按 MATH、三次右鍵、再按二。在卡西歐的圖形計算機中，按 OPTN，一次右鍵（F6）、PROB（F3）、nPr（F2）。

多數試算表軟體都有函式 PERMUT(Number，Number chosen)，用以計算置換。Number是描述物件數量的一個整數，Number chosen是描述每個置換中取物件數的整數。