廣義笛卡爾積
廣義笛卡爾積
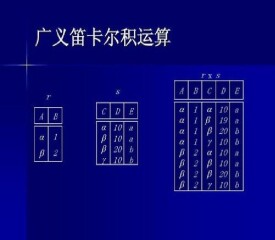
設兩個關係R和S的屬性列數分別是r和s,R和S的廣義笛卡爾積是一個(r+s)個屬性列的元組的集合,每一個元組的前r個分量來自R的一個元組,后s個分量來自S的一個元組。笛卡爾積記為R×S。形式定義為:R×S=t|t=∧tr∈R∧ts∈S 。

廣義笛卡爾積
設系,系,廣義笛卡積義:
目關係,前n列是關係R的屬性,后n列是關係S的屬性。每個元組的前n個屬性是關係R的一個元組,后m個屬性是關係S的一個元組。若關係R有p個元組,關係S有q個元組,關係有個元組,且每個元組的屬性為。兩隊游泳運動對均有3名隊員組成。現做循環比賽,賽事表可看成是兩對名單的廣義笛卡兒積。
現有關係R和關係S,如下表所示。
| 關係R | ||
|---|---|---|
| A | B | C |
| a1 | b1 | c1 |
| a1 | b2 | c2 |
| a2 | b2 | c1 |
| 關係S | ||
|---|---|---|
| A | B | C |
| a1 | b2 | c2 |
| a1 | b3 | c2 |
| a2 | b2 | c1 |
先求關係R和關係S的廣義笛卡兒積。
| RxS | |||||
|---|---|---|---|---|---|
| R.A | R.B | R.C | S.A | S.B | S.C |
| a1 | b1 | c1 | a1 | b2 | c2 |
| a1 | b1 | c1 | a1 | b3 | c2 |
| a1 | b1 | c1 | a2 | b2 | c1 |
| a1 | b2 | c2 | a1 | b2 | c2 |
| a1 | b2 | c2 | a1 | b3 | c2 |
| a1 | b2 | c2 | a2 | b2 | c1 |
| a2 | b2 | c1 | a1 | b2 | c2 |
| a2 | b2 | c1 | a1 | b3 | c2 |
| a2 | b2 | c1 | a2 | b2 | c1 |
觀察上關係可以看出是目的關係,前3列是關係R屬性,后3列是關係S的屬性,每個元組的前3個屬性是關係R的一個元組,后3個屬性是關係S的一個元組。關係個元組。