里德伯常量
里德伯常量
里德伯常量是原子物理學中的基本物理常量之一,為一經驗常數,一般取R=1.097373157×10^7m。里德伯常量起初是在為表示氫原子光譜的里德伯公式中引入的, 1/λ=R[(1/n)-(1/m)]。其中的R,即里德伯常量,實驗測得的數值為:R=1.0967758×10^7m。
1913年波爾推導出其理論值,為R=1.09737315689396×10^7m,與實驗值吻合得很好。
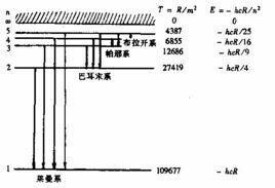
1885年,瑞士數學教師約翰·雅各布·巴爾默(J. J. Balmer)在一篇論文中報告了氫原子光譜的一個經驗規律:1/ λ= R[(1/2 )-(1/ n )],同時得出里德伯常量的近似數值。
1908年,德國物理學家弗里德里希·帕邢(Friedrich Paschen)發現了氫原子光譜的帕邢系。
1913年,丹麥物理學家尼爾斯·玻爾運用自己創立的原子模型和普朗克的量子學說第一次試圖計算推導出里德伯常量的精確值:
R=2π me/[(4π ε') ch ]
e是元電荷, h是普朗克常數, ε'為真空介電常數, m為電子質量。
計算后可得: R = 1.097373157×10^7m ,與實驗值誤差僅萬分之五。
玻爾把普朗克常數和里德起來,體現了聯繫的普遍性和特殊性,原子結構模型理論與原子光譜的本質聯繫為光譜學的發展奠定了基礎。