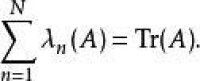跡類運算元
跡類運算元
在數學中,跡類運算元(英語:Trace class)是一個滿足如下條件的緊運算元,可以為其定義跡,使得跡有限且與基底的選擇無關。跡類運算元本質上與核型運算元相同,但是許多作者將希爾伯特空間上的核型運算元這一特殊情況稱為“跡類運算元”,而將“核型運算元”用於更一般的巴拿赫空間。
模擬矩陣的定義,在可分希爾伯特空間H上的有界線性運算元A被稱為屬於 跡類,如果對於H的所有標準正交基{e}
跡類運算元
跡類運算元
如果A是非負自伴運算元,我們也可以通過可能發散的求和將A的跡定義為擴展實數
跡類運算元
如果A是非負自伴運算元,當且僅當Tr(A)<∞時,A是跡類的。因此,自伴運算元A是跡類的,當且僅當其正部A和負部A都是跡類的。 (自伴運算元的正負部通過連續泛函演算得到。)
跡是跡類運算元空間上的線性泛函,即
跡類運算元
跡類運算元
如果A有界且B是跡類的,則AB和BA也是跡類的,且有
跡類運算元
跡類運算元
如果A是跡類的,則可以定義1+A的弗雷德霍姆行列式
跡類運算元
跡類運算元
其中 是A的譜。A的跡類條件保證這一無限乘積是有限的:實際上
跡類運算元
跡類運算元
跡類運算元
這還意味著 當且僅當 是可逆的。
跡類運算元
跡類運算元
跡類運算元
跡類運算元
跡類運算元
令A是可分希爾伯特空間H中的跡類運算元,並且令 為A的特徵值。假設 在計數時考慮了代數重數(即如果 的代數重數為k,則 在計數時被重複K次如)。Lidskii定理(以Victor Borisovich Lidskii命名)指出
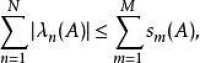
跡類運算元
跡類運算元
跡類運算元
在特徵值 和緊運算元A的奇異值 之間。