平均指標

反映現象總體的綜合特徵

平均指標亦稱“平均數”。同質總體內各單位某一數量標誌的一般水平。平均數的特點是對總體各單位之間標誌值的差異抽象化，用一個數字顯示其一般水平。因此，它可用來比較不同時間、地點或部門之間同類現象水平的高低，分析現象間的相互關係，估計推算其他有關指標，如用樣本平均每畝產量乘收穫面積估算農作物總產量。現象的同質性是計算平均數的前提條件，只有在同質總體內才能計算平均數。把平均數與分組法結合運用，用組平均數補充總平均數，對認識客觀現象有重要作用。在運用平均數時，還要注意利用分配數列和典型資料來加以補充。由於掌握資料和研究任務不同，平均數有算術平均數，調和平均數，幾何平均數、眾數和中位數等五種不同計算形式。

1簡述平均指標概念意義和作用

2原則 3種類數值平均數

位置平均數 4比較 5應用注意問題

簡述

平均指標概念

平均指標可以是同一時間的同類社會經濟現象的一般水平，稱為靜態平均數，也可以是不同時間的同類社會經濟現象的一般水平，稱為動態平均數。

意義和作用

平均指標在認識社會經濟現象總體數量特徵方面有重要作用，得到廣泛應用。

1、平均指標可以反映現象總體的綜合特徵。

2、平均指標可以反映分配數列中各變數值分佈的集中趨勢。

3、平均指標經常用來進行同類現象在不同空間、不同時間條件下的對比分析，從而反映現象在不同地區之間的差異，揭示現象在不同時間之間的發展趨勢。

原則

平均指標，是同類社會經濟現象總體內各單位某一數量標誌在一定時間、地點和條件下數量差異抽象化的代表性水平指標，其數值表現為平均數。平均指標是社會經濟統計中常用的綜合指標之一，具有很重要的作用，但是如果應用不當，平均指標可能會給我們帶來一些“困惑”、“假象”，使用時要注意以下原則：

如何才能避免這種“尷尬”呢?

一、必須注意所研究社會經濟現象約同質性同質性。

就是社會經濟性現象的各個單位在被平均的標誌上具有同類性。各單位之間的差別，僅僅表現在數量上，被平均的只是量的差異。馬克思指出：“平均量始終只是同種的很多不同的個別量的平均數。如果各單位在類型上是異質的，特別是從社會關係來說存在著根本差別，這樣，平均數不僅不能說明事物的本質和規律性，反而會歪曲事實，掩蓋真相，抹煞現象之間的本質差別，它只能是“虛構”的平均數。所以科學的平均指標應建立在分組法的基礎上，藉助於分組法來區分不同性質的總體，然後就同類總體計算和運用平均指標。

二、平均指標要與變異指標結合運用

平均指標確實能反映某種事物的一般水平，在比較不同空間和時間上的情況時能消除規模大小的影響，是衡量其差距的重要指標。但只依據平均指標來評價事物的優劣是遠遠不夠的。因為總體內部各單位標誌值具有差異，有高低、大小、多少之別。就總體而言，平均數背後隱藏最大值與最小值之間的差距，有的差距不大，有的則相差非常懸殊。總體內部各單位標誌值差距懸殊的平均數就掩蓋著尖銳的矛盾，讓人們感到不真實。所以，在反映具體問題時，除了列出總平均指標外還應把總體內部各單位標誌值中最大值、最小值及其差距擺出來，要列出平均差異大小和差異的相對程度，即要測定標誌變異指標。

三、必須注意用組平均數補充說明總平均數

根據同質總體計算的平均數是總平均數，它說明總體各個單位的一般水平，在統計分析中有重要作用。但是，僅看總平均數還不能全面說明總體特徵，因為總體單位之間還存在其他一些性質上的差別，有時被總平均數所掩蓋。為揭示一些重要差別，還必須注意各單位在性質上的差別對總平均數的影響作用，即需要按反映重要差別的標誌把總體單位分組，計算組平均數，以補充說明總平均數。

四、必須注意一般與個別相結合，把平均數和典型事例結合起來

任何事物的發展都是不平衡的，在同一總體中，既有先進部分，也有後進部分，不能滿足於一般狀況。如果在分析研究時，只掌握一般情況而忽視個別情況，不注意發現先進，找出後進，促使後進轉化，就會犯錯誤。所以，為了全面深入地認識事物，在應用平均數時，需要結合個別典型事物，研究先進和落後的典型，發現新生事物，加以總結推廣，推動事物的發展。

五、必須注意應用分配數列補充說明平均數

平均數的重要特徵是把總體各單位的數量差異抽象化，掩蓋了各單位的數量差別及分配狀況，因此，要用分配數列來補充說明平均數。

種類

平均指標按計算和確定的方法不同，分為算術平均數、調和平均數、幾何平均數、眾數和中位數。前三種平均數是根據總體各單位的標誌值計算得到的平均值，稱作數值平均數。眾數和中位數是根據標誌值在分配數列中的位置確定的，稱為位置平均數。

數值平均數

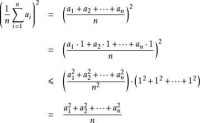
算術平均數

算術平均數也成均值，是最常用的平均指標。它的基本公式形式是總體標誌總量除以總體單位總量。在實際工作中，由於資料的不同，算術平均數有兩種計算形式：即簡單算術平均數和加權算術平均數。

⑴簡單算術平均數適用於未分組的統計資料，如果已知各單位標誌值和總體單位數，可採用簡單算術平均數方法計算。

⑵ 加權算術平均數適用於分組的統計資料，如果已知各組的變數值和變數值出現的次數，則可採用加權算術平均數計算。

加權算術平均數的大小受兩個因素的影響：其一是受變數值大小的影響。其二是各組次數佔總次數比重的影響。在計算平均數時，由於出現次數多的標誌值對平均數的形成影響大些，出現次數少的標誌值對平均數的形成影響小些，因此就把次數稱為權數。在分組數列的條件下，當各組標誌值出現的次數或各組次數所佔比重均相等時，權數就失去了權衡輕重的作用，這時用加權算術平均數計算的結果與用簡單算術平均數計算的結果相同。

調和平均數

調和平均數是總體各單位標誌值倒數的算術平均數的倒數，又稱為倒數平均數，由簡單調和平均數和加權調和平均數。

幾何平均數

幾何平均數是n個變數值乘積的n次方根。在統計中，幾何平均數常用於計算平均速度和平均比率。幾何平均數也有簡單平均和加權平均兩種形式。

位置平均數

眾數

眾數是指總體中出現次數最多的標誌值。眾數也是一種位置平均數。在實際工作中往往可以代表現象的一般水平，如市場上某種商品大多數的成交價格，多數人的服裝和鞋帽尺寸等，都是眾數。但只有在總體單位數多且有明顯的集中趨勢時，才可計算眾數。

中位數

將總體各單位的標誌按大小順序排列，處於中間位置的標誌值就是中位數。由於中位數是位置平均數，不受極端值的影響，在總體標誌值差異很大的情況下，中位數具有很強的代表性。

比較

平均指標的比較——眾數、中位數與算術平均數

算術平均數、中位數和眾數都是反映數據分佈集中趨勢的平均指標，他們各具特點：

算術平均數是根據所有數據計算的，中位數和眾數是根據數據分佈形狀和位置確定的；算術平均數只適用於定量的數據，中位數適用於定量和定序的數據，眾數適用於定量、定序和定類的數據，但有可能存在沒有眾數或多個眾數的情況；算術平均數易受到極端值的影響，有極端變數值時，用中位數和眾數作為代表值更好。

此外，眾數、中位數和算術平均數三者也存在一定的數量關係。在鐘形分佈中，眾數是分佈最高峰對應的變數值，一般中位數比較適中，算術平均數受極端變數值的影響，可能偏大也可能偏小。

應用注意問題

1、計算和應用平均指標必須注意現象總體的同質性。只有在同質總體的基礎上計算和應用平均指標，才有真是的社會經濟意義。如果根據不同性質總體的數據資料計算平均指標，就會掩蓋事物的本質差別，得到的平均數是虛構的平均數，不能真實反映現象的一般水平。

2、用組平均數補充說明平均數。

3、計算和運用平均數時，要注意極端數值的影響。

4、在運用平均數分析時還應注意用分配數列補充說明平均數。

5、把平均數與典型事例相結合。