連分數

完全商有如下簡單性質：①,一般地,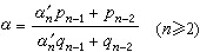；②αn=【αń】，n=0，1,2，…，由此可推出實數展成連分數時表法惟一。該實數為有理數時，規定最後一個αN>1。

循環連分數 設α=【α0,α1,…,αn,…】,如果l≥m時，對某個固定的正整數k,有αl=αl+k,那麼這樣的連分數叫做循環連分數，這種最小的 k叫做它的周期，記為。例如 等。運用漸近分數、完全商的性質以及抽屜原理,J.-L.拉格朗日證明了有關循環連分數的一個重要定理：一個連分數為循環連分數，則此數是某個有理係數的二次不可約多項式的根；反之亦然。

當D>0且不是平方數，則，其中函數【x】表示不超過x的最大整數。此外，設佩爾方程x2-Dy2=1的最小解為ε，則的周期k滿足。

應用舉例 連分數有許多應用。例如:①1891年,A.胡爾維茨證明了：在α 的三個連續漸近分數中必有一個適合。由此可得，任一無理數α，有無窮多個有理數。式中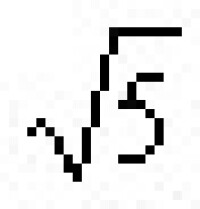是最佳的，即設，則必有一無理數α，使不能有無窮多個解，如就是這樣一個數；②設D>0且不是平方數,之連分數展開式中αń可表為，此處Pn及Qn皆為整數。設n是最小的正整數，使(-1)n-1Qn=1,則x=pn-1,y=qn-1是佩爾方程x2-Dy2=1的最小解;③利用連分數可以證明數論中一個著名的定理：設素數p呏1(mod4),則p可表為二整數的平方和；④在近似計算方面，如求多項式的根的近似值，等等。