決策矩陣

Pugh矩陣，選擇矩陣(selection matrix or grid)，問題矩陣(problem matrix)，問題選擇矩陣(problem selection matrix)，機會分析(opportunity anyalysis)，方法矩陣(solution matrix)，標準評價表(criteria rating form)，關鍵矩陣(criteria-hased matrix)

決策矩陣是風險型決策常用的分析手段之一，又被稱為“決策表”、“益損矩陣”、“益損表”、“風險矩陣”。

決策矩陣評價一系列的選擇並為其排序。小組首先設計一些評價標準，然後按照標準對每個選擇進行評價。它屬於L型矩陣的一種。

·當必須將一些選項限定為1個時；

·當要基於幾條標準作決策時；

·用列表削減法將得到的選擇減少至有限數目后。

·當需要致力解決一個問題或者只有一個改進機會時； ·當只能實施一種改進方法時；

·當只能開發一種新產品時。

1.狀態變數：指可能影響決策後果的各種客觀外界情況或自然狀態。是不可控因素。

2.決策變數：指決策者所採取的各種行動方案，是可控因素。

3.概率：指各種自然狀態出現的概率。

4.損益值：在一種自然狀態下選取某種方案所得結果的損益值。

決策矩陣由備選方案、自然狀態（及其發生的概率）和益損值所組成，一般用由實際問題給出的條件來列出矩陣決策表。在經營管理中，對決策問題的描述集中表現在決策矩陣上，決策分析就是以決策矩陣為基礎，運用不同的分析標準與方法，從若干個可行方案中選出最優方案。

1用頭腦風暴法得出適用的評價標準，這個過程最好有顧客參與。

2討論並修改評價標準，分清“必須要”和“必須不”。從這些標準中選出最重要的，可能要用到列表削減法及多輪投票法等方法。

3按照每個標準的重要程度給每個標準分配一個權重，總分為10分。權重的分配可以通過討論、投票完成。或者每個組員給每個標準分配一個權重，將每個標準得到的權重相加，按總權重和的大小排序。

4畫出L型矩陣。評價標準放在頂端，選項排列在左邊。習慣將條目少的項作為列項。

5按標準評價每個選項，有三種方案。

方案1：給每個標準設立等級，比如：

1，2，3： 1——稍微，2——部分，3——很大程度上

或1，2，3： 1——低，2——中，3——高

或1，2，3，4，5：1——一點，…，5——很多

或l，4，9： 1——低，4——中，9——高

確保設立的等級是一致的。寫下標準，並使最大值（5或3）表示最期望的選擇：對顧客有最大的影響、最重要、最容易、成功的可能性最大。

方案2：按照每個選項多大程度地符合標準來給選項排序。l表示與標準最不符合的選項。

方案3：決策矩陣：建立一個基準，可以是一個選擇或者當前的產品或者服務：對於每個標準，將每項選擇與基準比較進行評分，差（一1），相同(0)，好（+1）。也可以用更細緻的標準，比如“2，1，0，1，2”五個等級或者“3，2，1，0，－1，－2，－3”七個等級。同樣，正數表示想要達到的等級。

6將每個選項的排序與權重相乘，然後相加。得分最高的選項不一定是必選的選項，但是得分的相對大小對問題的討論是很有意義的，並能幫我們最終達成一致意見。

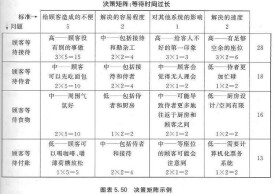
圖表5.50是“巴黎風情”酒店的顧客服務小組用來決定“等待時間過長”中哪一方面的問題應先解決的一個決策矩陣。問題出現在“顧客等待接待”、“顧客等待侍者”、“顧客等待食物”和“顧客等待付賬”幾個方面。

評價標準為“給顧客造成的不便”（多大程度上對顧客造成不良影響？）、“解決的容易程度”、“對其他系統的影響”和“解決的速度”。本來“解決的容易程度”常寫作“解決的困難程度”，但是那樣使排序反過來了。現在每個標準的最大值都表示最期望的選擇：給顧客帶來不便、易於解決、對其他系統有很大的影響，以及很快可以解決。

賦予“給顧客造成的不便”5分權重表示小組認為這是最重要的評價標準。“解決的容易程度”和“解決的速度”各有2分權重。“對其他系統的影響”有1分權重。

用3，2，1分別表示將每個問題分成高、中、低三個等級。例如：在問題“顧客等待食物”中，由於周圍氣氛很好，給顧客帶來的不便就評為中級(2)。因為它關係到侍者和廚房工作人員，這個問題不容易解決（1——不容易）。對其他系統的影響為中，因為這樣侍者必須更頻繁地去廚房。由於廚房設計得很擁擠且沒有柔性，故這個問題不能很快得到解決（1——低速）。（注意：小組假設解決方案要涉及廚房的重新設計，這可能是也可能不是一個很好的假設。）

將每個得分都與權重相乘。例如，“顧客等待接待”一項在“給顧客造成的不便”（權重為5）的問題上，評價為高(3)，那麼得分就為15。將每一排的得分相加得到每個問題的總分。“顧客等待接待”得到了最高分28。由於次高的得分是18，那麼選擇哪個就很顯然了。

同樣可以閱讀有關Medrad的案例，看看決策矩陣如何用來確定優先改進哪種問題。