馬可夫鏈
離散時間離散狀態的馬可夫過程
馬可夫鏈,因俄羅斯數學家安德烈·馬可夫得名,是離散時間離散狀態的馬可夫過程。
馬可夫鏈,因俄羅斯數學家安德烈·馬可夫(Андрей Андреевич Марков,1856年6月14日-1922年7月20日)得名,是離散時間離散狀態的馬可夫過程。在馬可夫過程(具有無後效性)中,在給定當前知識或信息的情況下,只有當前的狀態用來預測將來,過去(即當前以前的歷史狀態)對於預測將來(即當前以後的未來狀態)是無關的。與馬可夫鏈並列的馬可夫過程有泊松過程(時間連續,狀態離散)和維納過程(時間連續,狀態連續)。
而馬可夫鏈的所涉及的時間和狀態的分佈都離散,於是,馬可夫鏈可以看作一步一步、每一步對應不同狀態的集合。在馬可夫鏈的每一步,可以從一個狀態變到另一個狀態,也可以保持當前狀態,狀態的改變叫做過渡,與不同的狀態改變相關的概率叫做過渡概率(一步轉移概率)。例如,隨機漫步就屬於馬可夫鏈。隨機漫步中每一步的狀態是在圖形中的點,每一步可以移動到任何一個相鄰的點,在這裡移動到每一個點的概率都是相同的(無論之前漫步路徑是如何的)。
馬可夫在1906年首先做出了這類過程。而將此一般化到可數無限狀態空間是由柯爾莫果洛夫在1936年給出的。馬可夫鏈與布朗運動以及遍歷假說這兩個二十世紀初期物理學重要課題是相聯繫的,但馬可夫尋求的似乎不僅於數學動機,名義上是對於縱屬事件大數法則的擴張。
事實上,馬可夫過程的提出前,人們觀察到物理學中,很多確定性現象遵從如下演變原則:由時刻t0系統或過程所處的狀態,可以決定系統或過程在時刻t>t0所處的狀態,而無須藉助於t0以前系統所處的歷史狀態。如微分方程初值問題所描繪的物理過程就屬於這類確定性現象。把上述原則延伸到隨機現象,即當一物理系統或過程遵循的是以上原則或規律時,可引入統計規律概念“馬可夫性”或“無後效性”。
馬可夫鏈(Markov Chains) :
馬可夫鏈是隨機變數的一個數列。令隨機過程取有限或可數的正值,除非特殊說明,該過程的可能值集合將由非負整數集合來表示,當時我們稱該過程在時間n時的狀態為i.
假設該過程在狀態i,它達到下一個狀態j的概率是固定的。也就是說,對於所有的狀態以及所有的時間,其概率可表示為:
。
把滿足這樣條件的過程稱為 馬可夫鏈Markov Chain。
等式的的意義可理解為:對於一個馬科夫鏈,給定 過去的狀態和 當前的狀態,任意未來狀態的條件分佈與 過去的狀態是獨立的,而僅僅與 當前的狀態相關。
的值就是由當前的狀態i進入未來狀態j的概率。
例1:
假設明天下雨的幾率依賴今天是否下雨,而與過去的天氣無關。假設如果今天下雨了明天下雨的概率是α,如果今天不下雨明天下雨的概率是β。
可以定義下雨時狀態為0,不下雨時狀態為1,那麼以上描述的就是一個雙態馬可夫鏈問題,它的轉移概率如下所示:
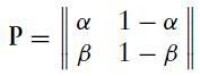
馬可夫鏈
構建一個馬可夫鏈)假設今天是否下雨依賴於過去兩天的天氣情況。特別的,假設過去兩天都下雨,那麼明天下雨的概率是0.7,如果今天下雨昨天沒下雨,那麼明天下雨的概率是0.5,如果今天沒下雨,昨天下了雨,明天下雨的概率是0.4,如果過去兩天都沒下雨,那麼明天下雨的概率是0.2.
如果我們令時刻的狀態僅僅依賴於n時刻是否下雨,那麼以上的描述就不是一個馬可夫鏈。但是,我們可以構建一個馬可夫鏈:任意時刻的狀態是由過去兩天的天氣情況確定的。也就是說,這個隨機過程有如下4種狀態:
狀態0 今天昨天都下雨了
狀態1 今天下雨昨天沒下雨
狀態2 今天沒下雨昨天下雨
狀態3 今天昨天都沒下雨

馬可夫鏈
例3:
random walk 隨機遊走)對於滿足 狀態空間為且,其中。這樣的馬可夫鏈稱為隨機遊走。該模型可以用來描述一個人在一條直線上行走,在任意一個點他往右的概率p或往左走的概率為。
例4:
假設有無窮多個瓶子,我們當前標以0,1,每一個瓶子放不同個數球,每瓶中的球都標以的,等(不同的球可以有相同的“編號),假設我們從標以0的瓶中隨便抽一個球,則此球的“編號什麼BJ,我們再從第j個瓶中抽取-球,若此球”編號什麼BK,我們當前再從第ķ個瓶中抽取一球,……這樣一直做下去,我們就得到一個馬可夫鏈。原因和前面幾個例子相同。事實上任一個馬可夫鏈都和這個模型等價,我們只要適當的選取每個瓶中球的個數,同時加以適當的編號,我們就可得取第一和第二個例子。
例5:
考慮以下股票模式,若股票上漲則明天會上漲的幾率為0.7;若股價下跌則明天會上漲的幾率為0.5。
這是一個馬可夫鏈,狀態0代表上漲,而狀態1代表股票下跌。
轉換矩陣為:
0.7 0.3
假設一個賭者有$1,而且每次賭贏$1的幾率為p,或賭輸$1的幾率為1-p。
這個賭博當其中一位賭者累積為$3或破產($0)就停止。
這個模式是馬可夫鏈,狀態相當於賭者手上的錢,即$0,$1,$2,$3,及其轉換矩陣為:1 0 0 0
0 p 0
0 0 0 1
馬可夫鏈通常用來建模排隊理論和統計學中的建模,還可作為信號模型用於熵編碼技術。
馬可夫鏈也有眾多的生物學應用,特別是增殖過程,可以幫助模擬生物增殖過程的建模。隱蔽馬可夫鏈還被用於生物信息學,用以編碼區域或基因預測。
馬可夫鏈最近的應用是在地理統計學中。其中,馬爾可夫鏈用在基於觀察數據的二到三維離散變數的隨機模擬。這一應用類似於“克里金”地理統計學(Kriging geostatistics),被稱為是“馬可夫鏈地理統計學”。
谷歌所使用的網頁排序演演算法(PageRank)就是由馬可夫鏈定義的。馬可夫模型也被應用於分析用戶瀏覽網頁的行為。
馬可夫過程,能為給定樣品文本,生成粗略,但看似真實的文本:他們被用於眾多供消遣的“模仿生成器”軟體。馬可夫鏈還被用於譜曲。
