拉格朗日乘子
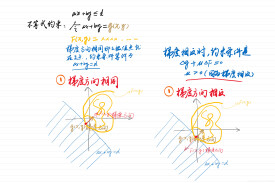
拉格朗日乘子
基本的拉格朗日乘子法(又稱為拉格朗日乘數法)，就是求函數f(x1,x2,...)在g(x1,x2,...)=0的約束條件下的極值的方法。其主要思想是引入一個新的參數λ（即拉格朗日乘子），將約束條件函數與原函數聯繫到一起，使能配成與變數數量相等的等式方程，從而求出得到原函數極值的各個變數的解。另外，可以將這種把約束條件乘以λ（即不定乘子）后加到待求函數上的求極值方法推廣到變分極值問題及其它極值問題當中，理論力學當中對非完整約束的處理方法就是利用變分法當中的拉格朗日乘子法。因為∂F/∂M=λ，當M增加或減少一個單位值時，F會相應變化λ。此時λ便代表，當成本條件改變時，工廠可達到的生產量最大值的變化率。
目錄
拉格朗日乘子法拉格朗日乘子（Lagrange multiplier）
基本的拉格朗日乘子法(又稱為拉格朗日乘數法)，就是求函數f(x1,x2,...)在g(x1,x2,...)=0的約束條件下的極值的方法。其主要思想是引入一個新的參數λ（即拉格朗日乘子），將約束條件函數與原函數聯繫到一起，使能配成與變數數量相等的等式方程，從而求出得到原函數極值的各個變數的解。
具體方法：
假設需要求極值的目標函數 (objective function) 為 f(x,y)，限制條件為 φ(x,y)=M
設g(x,y)=M-φ(x,y)
定義一個新函數
F(x,y,λ)=f(x,y)+λg(x,y)
則用偏導數方法列出方程：
∂F/∂x=0
∂F/∂y=0
∂F/∂λ=0
求出x,y,λ的值，代入即可得到目標函數的極值
擴展為多個變數的式子為：
F(x1,x2,...λ)=f(x1,x2,...)+λg(x1,x2...)
則求極值點的方程為：
∂F/∂xi=0（xi即為x1、x2……等自變數）
∂F/∂λ=g(x1,x2...)=0
以上內容在《數學手冊》當中有。另外，可以將這種把約束條件乘以λ（即不定乘子）后加到待求函數上的求極值方法推廣到變分極值問題及其它極值問題當中，理論力學當中對非完整約束的處理方法就是利用變分法當中的拉格朗日乘子法。
拉格朗日乘子法的用途：
從徠經濟學的角度來看，λ代表當約束條件變動時，目標函數極值的變化。因為∂F/∂M=λ，當M增加或減少一個單位值時，F會相應變化λ。
例如，假設目標函數代表一個工廠生產產品的數量，約束條件限制了生產中投入的原料和人力的總成本，我們求目標函數的極值，就是要求在成本一定的條件下，如何分配利用人力和原料，從而使得生產量達到最大。此時λ便代表，當成本條件改變時，工廠可達到的生產量最大值的變化率。
基本信息
- 中文名
- 拉格朗日乘子
- 外文名
- Lagrange multiplier
- 注音
- 求函數約束條件下的極值
- 別名
- 拉格朗日乘數法
- 所屬學科
- 數理科學
- 類型
- 數學計算方法