曲線方程
分為二維、三維曲線的方程
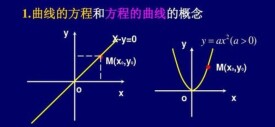
在直角坐標系中,如果某曲線C上的點與一個二元方程f(x,y)=0的實數解建立了如下的關係:(1)曲線上點的坐標都是這個方程的解;(2)以這個方程的解為坐標的點都是曲線上的點。那麼,這個方程叫做曲線的方程。
求曲線方程的步驟如下:
(1)建立適當的坐標系,用有序實數對(x,y)表示曲線上任意一點M的坐標;
(2)寫出適合條件的p(M)的集合;
(3)用坐標表示條件p(M),列出方程;
(4)化方程為最簡形式;
(5)驗證(審查)所得到的曲線方程是否保證純粹性和完備性。
這五個步驟可簡稱為:建系、設點、列式、化簡、驗證。
①直接法
②定義法
③相關點法
④向量
曲線:任何一根連續的線條都稱為曲線,包括直線、折線、線段、圓弧等。
按照經典的定義,從(a,b)到R3中的連續映射就是一條曲線,這相當於是說:
(1)R3中的曲線是一個一維空間的連續像,因此是一維的。
(2)R3中的曲線可以通過直線做各種扭曲得到。
(3)說參數的某個值,就是說曲線上的一個點,但是反過來不一定,因為我們可以考慮自交的曲線。
微分幾何就是利用微積分來研究幾何的學科,為了能夠應用微積分的知識,我們不能考慮一切曲線,甚至不能考慮連續曲線,因為連續不一定可微。這就要我們考慮可微曲線。但是可微曲線也是不太好的,因為可能存在某些曲線,在某點切線的方向不是確定的,這就使得我們無法從切線開始入手,這就需要我們來研究導數處處不為零的這一類曲線,我們稱它們為正則曲線。
正則曲線才是經典曲線論的主要研究對象。
曲線是1-2維的圖形,參考《分數維空間》。
處處轉折的曲線一般具有無窮大的長度和零的面積,這時,曲線本身就是一個大於1小於2維的空間。
基本性質1:等式兩邊同時加(或減)同一個數或同一個代數式,所得的結果仍是等式。
用字母表示為:若,c為一個數或一個代數式。則:
(1)
(2)
基本性質2:等式的兩邊同時乘或除以同一個不為0的數所得的結果仍是等式。
(3)若,則(等式的對稱性)
(4)若,則(等式的傳遞性)
含有未知數的等式叫方程。
方程可分為:整式方程和分式方程。
整式方程:方程的兩邊都是關於未知數的整式的方程叫做整式方程。
分式方程:分母中含有未知數的方程叫做分式方程。
方程的解:使方程左右兩邊相等的未知數的值叫做方程的解。
解方程:求方程的解的過程叫做解方程。
解方程的依據:1.移項; 2.等式的基本性質; 3.合併同類項; 4. 加減乘除各部分間的關係。
解方程的步驟:1.能計算的先計算; 2.轉化——計算——結果
例如:
移項:把方程中的某些項改變符號后,從方程的一邊移到另一邊,這種變形叫做移項,根據是等式的基本性質1。