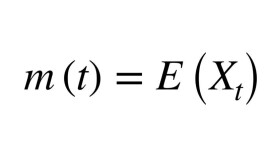均值函數
隨機過程的重要數量特徵
均值函數即一階原點矩函數過程的數學期望作為參數的函數。給定隨機過程 ，如果對於每個參數 ，隨機變數都是可積的，則稱上的函數為過程的均值函數。
[moment function]
矩函數是隨機過程有窮維分佈的矩。
對於給定的隨機過程 ，稱 的r元函數 為過程的r階原點矩函數（r-order original moment function）。
稱為過程的r階中心矩函數（r-order central moment function）。這裡總假設所涉及的矩存在。
矩函數是用來表述隨機過程在各個參數上的相互關係的數字特徵。最常用的是一、二階矩函數。r階矩函數更一般的形式為， ， ，其中， 。
基本信息
- 中文名
- 均值函數
- 外文名
- mean function
- 定義
- 隨機過程的重要數量特徵
- 適用範圍
- 數理科學
- 例如
- 矩函數