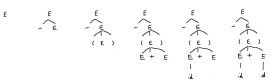
最左推導
數學領域中的推導公式
最左推導:若x和y是符號串α中有兩個以上的非終結符號時,對推導的每一步堅持把α中的最左非終結符號進行替換,稱為最左推導。
推導:x和y是符號串,若使用若干次產生式可以從x變換出y,則稱x推導出y(或者說y是x的推導),記為xy。
歸約:推導的逆過程稱之為歸約。
對於一給定的文法來說,從其開始符號到某一句型,或從一個句型到另一句型間的推導序列可能不惟一。例如對句型可以有如下幾個推導序列:
式子(2-3)
式子(2-4)
式子(2-5)
為了使句型或句子能按一種確定的推導序列來產生,通常人們可僅考慮最左推導或最右推導。所謂最左(右)推導,是指對於一個推導序列中的每一直接推導,被替換的總是當前符號串中的最左(右)非終結符號。例如,在上面的各推導序列中,式(2-4)和式(2-5)就分別是最左和最右推導。形式上,設有符號串α到符號串β的一個推導序列
其中,表示這個推導序列中的任一步直接推導,若總有,則此推導序列為最左推導;而總有時則為最右推導。通常,人們把能由最左(右)推導推出的句型稱為左(右)句型。另外,也常把最右推導稱為規範推導,而把右句型稱為規範句型。
然而,應當指出,對於文法中的每一句子都必定有最左和最右推導,但對一句型來說則不盡然,例如,對於上述文法G2[E]中的句型而言,僅有惟一的推導
顯然,推導既非最左推導亦非最右推導,故句型既不可能是左句型也不可能是規範句型。
對於一個給定的終結符號串w,若採用自頂向下的語法分析來判明w是否為某一語言L(G)中的句子,通常的做法乃是:試圖為w建立一個從G的開始符號S到w的最左推導。顯然,在建立此種推導序列的某一步,若當前被替換的非終結符號U是由若干個候選式定義的,即有,那麼,就必然會出現如何選用候選式的問題。一種辦法是逐個用這些候選式進行試探,以期獲得正確的選擇,即若用某一個αi替換U能使分析進行下去,則沿此路徑繼續前進;若一旦發現此選擇有錯,則廢棄由此選擇已做過的分析工作,並回退到出錯點再用下一個繼續進行試探,如此等等。因為使用這種方法需反覆地回退到出錯點進行試探,故稱為帶回溯的自頂向下的分析方法。由於回溯,將使語法分析的效率大大降低,故應設法予以避免。在第4章中,人們將介紹解決這一問題的途徑和方法。
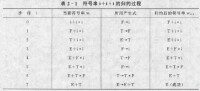
表2-1
這裡,人們經過了8步最左直接歸約,將符號串歸約為G2[E]的開始符號E,從而再一次證實了它是L(G2)中的一個句子。同時,容易看到,如果人們把上述歸約過程的各步所得的各個符號串按歸約過程的逆序寫出(也就是按上述過程的逆序來使用所使用過的產生式),那麼,實際上人們就得到了形如式(2?5)的最右推導。由此可見,最右(左)推導的逆過程是最左(右)歸約,反之亦然。因此,通常人們也將最左歸約稱為規範歸約。至於直接歸約、歸約以及最左(右)歸約的形式定義人們就不再贅述了,讀者不難仿照定義2?2和2?3給出。
此外,再看錶21中所列的第5步直接歸約。此時的符號串為,除了按產生式F→i把此符號串約為外,還可考慮按產生式或分別將歸約為和。但是,如果把后兩個符號串繼續進行歸約,當分別得到符號串E*E和E+E*E時,顯然已無法再進行歸約。也就是說,對符號串而言,i是惟一可被歸約的最左子串。於是,人們自然會提出這樣的問題,對於規範歸約的每一步,如何確定符號串中當前應被歸約的最左子串?這一問題,人們將在2?3?3中進行討論。