解核是由n次迭核經過求和而得到的一種核。核是位勢論的基本概念。在位勢論中,所謂核,常指一般位勢的核。
解核是由n次迭核經過求和而得到的一種核。
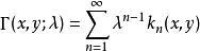
解核
設k(x,y)是k(x,y)的n次迭核,λ為實數或複數,則稱為解核。
設k(x,y)連續,|k(x,y)|≤M,則當時,具有線性積分運算元的方程存在惟一解,並且該解可以用解核表示為
(iterated kernel)
迭核是由已知核經過逐次積分而得到的各種核。
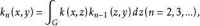
解核
設k(x,y)是線性積分運算元的核,令k(x,y)=k(x,y),用歸納法定義:則稱k(x,y)是k(x,y)的n次迭核。