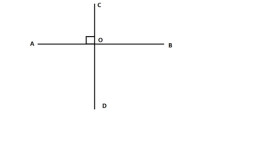
垂線

從直線外一點到這條直線的垂線段的長度，稱之點到直線的距離，若兩條直線相交，且相交后的四個角都為90°，則這兩條直線互相垂直，即為互為垂線。

垂線的定義中，只是規定了兩直線交角的大小(90°)，並沒有規定兩條直線的位置如何。也就是說，不論一條直線的位置如何，只要另一條與它的交角是90°，其中任何一條直線就是另一條直線的垂線。

垂線的基本性質是：

（1）過直線上或直線外的一點，有且只有一條直線和已知直線垂直。

（2）從直線外一點到這條直線上各點所連的線段中，垂直線段最短。

從直線外一點到這條直線的垂線段的長度，叫做點到直線的距離。顯然，垂線段是指以直線外一點與垂足為兩端點的線段。在連接直線外一點與直線上的所有點的連線中，垂線段最短，簡稱垂線段最短。在同一平面內，過一點有且只有一條直線與已知直線垂直。

垂線和鉛垂線

當兩條直線相交所成的四個角中，有一個角是直角時，就說這兩條直線互相垂直，條直線的垂線其中的一條直線叫做另一條線的垂線。

事實上，老師在講“垂線”的概念時，總喜歡用鉛垂線引入。說瓦工師傅砌牆時，為了使牆砌得與地面垂直，先吊一根鉛垂線，即用一根細線吊一個重鎚，重鎚由於地球引力，呈與地面水平線垂直的狀態下垂。這時，鉛垂線與水平線但是，由於水平線、鉛垂線的位置特殊，也給學生帶來一些副作用，今後一提到垂線，總以為處於鉛垂線的狀態，從而帶來不便。如梯形，源於生活中常見的梯子。但梯子在使用時，總是放成一種特殊的位置，由此在大腦中形成梯形的典型位置，即梯形上下底處於水平位置，而對梯形的本質定義：“一雙對邊平行，另一雙對邊不平行的四邊形”就比較陌生，一旦看到梯形的變式圖形，就很不習慣了。

學幾何概念，常常從生活實例引入，這是很必要的。因為幾何本來就來源於實踐。實例可以幫助我們理解概念，形成概念。幾何概念來源於生活，卻高於生活。在實例的基礎上，一定要上升到幾何概念的本質，從本質屬性上去掌握概念，擺脫實例的局限性，避免在概念理解上的特殊化。