角加速度
角速度的變化率
質點繞某軸轉動時,角速度也可能隨時間變化。我們把單位時間內角速度的變化量叫作角加速度。
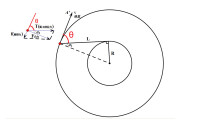
角加速度圖解
α=Δω/Δt
弧度/秒²(rad/s²)
角加速度意味著什麼呢?想象一個靜止的旋轉木馬。因為它沒在旋轉,它的角速度為零。現在你啟動,使它以每4秒1轉,即0.25r/s的速度旋轉。於是旋轉木馬的角速度變為非零。其後若是保持此轉速不變,那麼它的角加速度便是零。
我們可以用正、負號表示角速度與角加速度的方向,約定角速度和角加速度的方向與轉軸方向平行時取正號,反向平行時取負號。
轉動剛體從瞬時t開始的角速度變化Δω與相應時間間隔Δt的比值稱為平均角加速度,即α=Δω/Δt。
若Δt→0,則這一比值就稱為在瞬時t剛體轉動的角加速度,又稱瞬時角加速度,記為ε,即ε=limεm)(Δt→0=Δω/Δt.當作用於物體的力矩是常數時,角加速度也會是常數.在這個等角加速度的特別狀況里,此運動方程式會算出一個決定性的,單值的角加速度.當作用於物體的力矩不是常數時,物體的角加速度會隨時間而變.這方程式成為一個微分方程式.這微分方程式是此物體的運動方程式;它可以完全的描述此物體的運動.
平面運動下,角加速度——作為角速度的變化率——也可以類似的定義為一個標量。我們可以說一個運動是順時針轉動加速或者逆時針轉動加速。
角加速度
ω=r×V
上式每個物理量都應該有矢量符號。角加速度與加速度類似,就是角速度的變化率。由於角速度具有矢量性,角加速度也具有矢量性。
從運動學上我們就可以通過對上式求微商來得到角加速度的大小與方向。注意,由於r一般隨時間變化,因此角加速度一般不等於r×a。而如果運動固定為圓周運動,r是一個常數,那麼角加速度就等於ra,方向則是r×a的方向。
我們發現,二維平面的運動使得上述矢量叉乘的結果必然在垂直於該平面的方向,如果一個矢量的方向固定在某一直線上,那其表現也確實與標量很是類似。
加速度是速度的變化,所以角加速度的單位是弧度每秒每秒。同樣,因為弧度無量綱,於是角加速度的單位可寫作1/s。在所有這些方面,角運動和線性運動都是能平行對應的。速度等於位置的變化除以時間的變化,同樣,角速度等於角位置的變化除以時間的變化。
角加速度描述角速度變化快慢和方向的物理量。如果物體的角速度是改變的,就說這個物體具有角加速度。
動錐的瞬時角加速度定義為瞬時角速度對時間的導數。