尺寸公差
允許的上下偏差之差大小
尺寸公差簡稱公差,是指允許的,最大極限尺寸減最小極限尺寸之差的絕對值的大小,或允許的上偏差減下偏差之差大小。尺寸公差是一個沒有符號的絕對值。極限偏差=極限尺寸-基本尺寸,上偏差=最大極限尺寸-基本尺寸,下偏差=最小極限尺寸-基本尺寸。
尺寸公差是指在切削加工中零件尺寸允許的變動量。在基本尺寸相同的情況下,尺寸公差愈小,則尺寸精度愈高。
尺寸公差是指在零件製造過程中,由於加工或測量等因素的影響,完工後的實際尺寸總存在一定的誤差。為保證零件的互換性,必須將零件的實際尺寸控制在允許變動的範圍內,這個允許的尺寸變動量稱為尺寸公差。
例:
1,基本尺寸設計給定的尺寸:30mm
2,極限尺寸允許尺寸變動的兩個極限值:
最大極限尺寸=30+0.01=30.01mm
最小極限尺寸=30-0.01=29.99mm
3,極限偏差極限尺寸減基本尺寸所得的代數值。即最大極限尺寸和最小極限尺寸減基本尺寸所得的代數差,分別為上偏差和下偏差,統稱極限偏差。孔的上、下偏差分別用大寫字母ES和EI表示:
上偏差ES=30.01-30=+0.01
下偏差EI=29.99-30=-0.01
4,尺寸公差:允許尺寸的變動量,即最大極限尺寸減最小極限尺寸,也等於上偏差減下偏差所得的代數差。尺寸公差是一個沒有符號的絕對值。
公差:30.01-29.99=0.02
或0.01-(-0.01)=0.02
國標GB1800.1-2009將確定尺寸精度的標準公差等級分為18級,分別用IT1、IT2、……IT18表示。從IT1到IT18相應的公差數值依次加大、精度依次降低。
切削加工所獲得的尺寸精度一般與使用的設備、刀具和切削條件等密切相關。尺寸精度愈高,零件的工藝過程愈複雜,加工成本也愈高。因此在設計零件時,應在保證零件的使用性能的前提下,盡量選用較低的尺寸精度。
基本尺寸0至500mm標準公差數值表(摘自GB/T1800.1-2009)
| 基本尺寸 | 公差值 | ||||||||||||||||||
| 微米 | 毫米 | ||||||||||||||||||
| > | = | IT1 | IT2 | IT3 | IT4 | IT5 | IT6 | IT7 | IT8 | IT9 | IT10 | IT11 | IT12 | IT13 | IT14 | IT15 | IT16 | IT17 | IT18 |
| 3 | 0.8 | 1.2 | 2 | 3 | 4 | 6 | 10 | 14 | 25 | 40 | 60 | 0.1 | 0.14 | 0.25 | 0.4 | 0.6 | 1 | 1.4 | |
| 3 | 6 | 1 | 1.5 | 2.5 | 4 | 5 | 8 | 12 | 18 | 30 | 48 | 75 | 0.12 | 0.18 | 0.3 | 0.48 | 0.75 | 1.2 | 1.8 |
| 6 | 10 | 1 | 1.5 | 2.5 | 4 | 6 | 9 | 15 | 22 | 36 | 58 | 90 | 0.15 | 0.22 | 0.36 | 0.58 | 0.9 | 1.5 | 2.2 |
| 10 | 18 | 1.2 | 2 | 3 | 5 | 8 | 11 | 18 | 27 | 43 | 70 | 110 | 0.18 | 0.27 | 0.43 | 0.7 | 1.1 | 1.8 | 2.7 |
| 18 | 30 | 1.5 | 2.5 | 4 | 6 | 9 | 13 | 21 | 33 | 52 | 84 | 130 | 0.21 | 0.33 | 0.52 | 0.84 | 1.3 | 2.1 | 3.3 |
| 30 | 50 | 1.5 | 2.5 | 4 | 7 | 11 | 16 | 25 | 39 | 62 | 100 | 160 | 0.25 | 0.39 | 0.62 | 1 | 1.6 | 2.5 | 3.9 |
| 50 | 80 | 2 | 3 | 5 | 8 | 13 | 19 | 30 | 46 | 74 | 120 | 190 | 0.3 | 0.46 | 0.74 | 1.2 | 1.9 | 3 | 4.6 |
| 80 | 120 | 2.5 | 4 | 6 | 10 | 15 | 22 | 35 | 54 | 87 | 140 | 220 | 0.35 | 0.54 | 0.87 | 1.4 | 2.2 | 3.5 | 5.4 |
| 120 | 180 | 3.5 | 5 | 8 | 12 | 18 | 25 | 40 | 63 | 100 | 160 | 250 | 0.4 | 0.63 | 1 | 1.6 | 2.5 | 4 | 6.3 |
| 180 | 250 | 4.5 | 7 | 10 | 14 | 20 | 29 | 46 | 72 | 115 | 185 | 290 | 0.46 | 0.72 | 1.15 | 1.85 | 2.9 | 4.6 | 7.2 |
| 250 | 315 | 6 | 8 | 12 | 16 | 23 | 32 | 52 | 81 | 130 | 210 | 320 | 0.52 | 0.81 | 1.3 | 2.1 | 3.2 | 5.2 | 8.1 |
| 315 | 400 | 7 | 9 | 14 | 18 | 25 | 36 | 57 | 89 | 40 | 230 | 360 | 0.57 | 0.89 | 1.4 | 2.3 | 3.6 | 5.7 | 8.9 |
| 400 | 500 | 8 | 10 | 16 | 20 | 27 | 40 | 63 | 97 | 155 | 250 | 400 | 0.63 | 0.97 | 1.55 | 2.5 | 4 | 6.3 | 9.7 |
研究背景
公差幾乎貫穿了整個產品的生命周期,影響著產品的質量、加工工藝路線、檢測、生產製造成本及最終產品的裝配等。然而,現有CAD系統雖能提供對實際物體精確的數學表示,但公差信息只是一種符號式的表示,缺少有效的工程語義,沒有包含對下游工作有用的全部信息,難以真正實現CAD,CAPP和CAM的集成。CAD,CAPP和CAM的集成需要在系統中包含公差信息,並且能對所包含的公差信息作出正確合理的解釋,這也是公差信息建模與表示的任務。計算機輔助公差設計自20世紀70年代末提出以來,對公差信息建模的數學模型已有了大量的研究,基於數學定義的公差數學模型是研究熱點之一。研究將SDT(small displacement torsor)應用到公差建模中,提出一種新的平面尺寸公差建模方法。根據約束條件將平面尺寸公差分為2類,並應用SDT來描述公差域,建立相應尺寸公差的數學模型,並且用此模型對公差綜合進行驗證。
平面尺寸公差分類
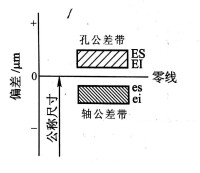
圖1 尺寸公差的分類
尺寸公差是分配到一對要素(點、線、面)間的公差,對每一要素,其上的所有點必須位於相距一定距離的1對平行平面(直線)間,而2對平行平面(直線)之間的距離等於給定的尺寸公差。
ASME中沒有對尺寸公差進行嚴格明確的數學定義,要建立尺寸公差域,必須與其他已定義的公差類型一樣,用數學矢量方程來定義尺寸公差。設T,T為尺寸公差的上限和尺寸公差的下限,兩尺寸公差域中心面的位置矢量可能是固定的(對I類組成環),也可能是不固定的(對II類組成環),尺寸公差域的位置可能會沿尺寸公差域的平行平面(直線)的方向上有一個平動位移。
平面尺寸公差建模

圖2 公差綜合的裝配示意圖
公差綜合是在滿足產品裝配技術要求下確定各組成環之間的經濟合理的公差。在前述尺寸公差模型的基礎上,只需給定SDT中各分量,即可得到尺寸公差值。圖2是一個簡單的裝配示意圖,零件1的配合尺寸無約束,零件2的配合尺寸有約束,2個零件裝配起來,現確定相關尺寸的公差。