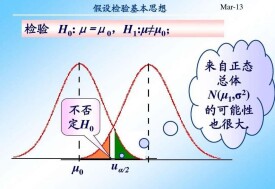
假設檢驗中的兩類錯誤
數理統計學中的名詞
假設檢驗及其兩類錯誤是數理統計學中的名詞。在進行假設檢驗時提出原假設和備擇假設,原假設實際上是正確的,但我們做出的決定是拒絕原假設,此類錯誤稱為第一類錯誤。原假設實際上是不正確的,但是我們卻做出了接受原假設的決定,此類錯誤稱為第二類錯誤。
假設檢驗中的兩類錯誤是指在假設檢驗中,由於樣本信息的局限性,勢必會產生錯誤,錯誤無非只有兩種情況,在統計學中,我們一般稱為Ⅰ類錯誤,Ⅱ類錯誤。
右圖是研究結論和實際情況關係的矩陣:
| 實際情況 | |||
| H0正確 | H0錯誤 | ||
| 研究結論 | 拒絕H0 | I類錯誤 | 正確 |
| 接受H0 | 正確 | II類錯誤 | |
第一類錯誤( Ⅰ類錯誤)也稱為 α錯誤,是指當虛無假設(H0)正確時,而拒絕H0所犯的錯誤。這意味著研究者的結論並不正確,即觀察到了實際上並不存在的處理效應。
可能產生原因:
1、樣本中極端數值。
2、採用決策標準較寬鬆。
第二類錯誤( Ⅱ類錯誤)也稱為β錯誤,是指虛無假設錯誤時,反而接受虛無假設的情況,即沒有觀察到存在的處理效應。
可能產生的原因:
1、實驗設計不靈敏。
2、樣本數據變異性過大。
3、處理效應本身比較小。
兩類錯誤的關係:
1、 α+β不一定等於1。
2、在樣本容量確定的情況下,α與β不能同時增加或減少。
3、統計檢驗力。(1-β)
犯Ⅰ類錯誤得危害較大,由於報告了本來不存在的現象,則因此現象而衍生出的後續研究、應用的危害將是不可估量的。相對而言,Ⅱ類錯誤的危害則相對較小,因為研究者如果對自己的假設很有信心,可能會重新設計實驗,再次來過,直到得到自己滿意的結果(但是如果對本就錯誤的觀點堅持的話,可能會演變成Ⅰ類錯誤)。