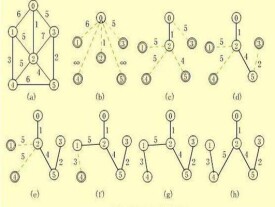
最小生成樹

最小生成樹

最小生成樹其實是最小權重生成樹的簡稱。一個有n個結點的連通圖的生成樹是原圖的極小連通子圖，且包含原圖中的所有n個結點，並且有保持圖連通的最少的邊。最小生成樹可以用kruskal（克魯斯卡爾）演演算法或Prim（普里姆）演演算法求出。最小生成樹性質：設G=(V，E）是一個連通網路，U是頂點集V的一個非空真子集。根據樹的定義，則T中必有一條從紅點u到藍點v的路徑P，且P上必有一條紫邊（u'，v'）連接紅點集和藍點集，否則u和v不連通。當一條邊（u，v）加入T時，必須保證T∪(u，v)仍是MST的子集，我們將這樣的邊稱為T的安全邊。

目錄
1應用 2性質 說明
證明 3演算法描述 偽代碼
Prim演算法 Kruskal演算法 C語言代碼
kruskal Prim

應用

生成樹和最小生成樹有許多重要的應用。
例如：要在n個城市之間鋪設光纜，主要目標是要使這 n 個城市的任意兩個之間都可以通信，但鋪設光纜的費用很高，且各個城市之間鋪設光纜的費用不同，因此另一個目標是要使鋪設光纜的總費用最低。這就需要找到帶權的最小生成樹。

性質

說明

最小生成樹性質：設是一個連通網路，U是頂點集V的一個非空真子集。若(u，v）是G中一條“一個端點在U中（例如：），另一個端點不在U中的邊（例如：），且（u，v）具有最小權值，則一定存在G的一棵最小生成樹包括此邊（u，v）。

證明

為方便說明，先作以下約定：
①將集合U中的頂點看作是紅色頂點，②而V-U中的頂點看作是藍色頂點，③連接紅點和藍點的邊看作是紫色邊，④權最小的紫邊稱為輕邊（即權重最"輕"的邊）。於是，MST性質中所述的邊（u，v）就可簡稱為輕邊。
用反證法證明MST性質：
假設G中任何一棵MST都不含輕邊（u，v）。則若T為G的任意一棵MST，那麼它不含此輕邊。
根據樹的定義，則T中必有一條從紅點u到藍點v的路徑P，且P上必有一條紫邊（u'，v'）連接紅點集和藍點集，否則u和v不連通。當把輕邊（u，v）加入樹T時，該輕邊和P必構成了一個迴路。刪去紫邊（u'，v'）后迴路亦消除，由此可得另一生成樹T'。
T'和T的差別僅在於T'用輕邊（u，v）取代了T中權重可能更大的紫邊（u'，v'）。因為，所以
即T'是一棵比T更優的MST，所以T不是G的MST，這與假設矛盾。
所以，MST性質成立。

演演算法描述

求MST的一般演演算法可描述為：針對圖G，從空樹T開始，往集合T中逐條選擇並加入條安全邊（u，v），最終生成一棵含條邊的MST。
當一條邊（u，v）加入T時，必須保證仍是MST的子集，我們將這樣的邊稱為T的安全邊。

偽代碼

GenerieMST(G){//求G的某棵MST
T〈-￠； //T初始為空，是指頂點集和邊集均空
while T未形成G的生成樹 do{
找出T的一條安全邊（u，v）；//即T∪{(u，v)}仍為MST的子集
T=T∪{(u，v)}； //加入安全邊，擴充T
}
return T； //T為生成樹且是G的一棵MST
}
注意：
下面給出的兩種求MST的演演算法均是對上述的一般演演算法的求精，兩演演算法的區別僅在於求安全邊的方法不同。
為簡單起見，下面用序號0，1，…，來表示頂點集，即是：
，
G中邊上的權解釋為長度，並設。
求最小生成樹的具體演演算法（pascal):

Prim演演算法

procedure prim(v0:integer);
var
lowcost,closest:array[1..maxn] of integer;
i,j,k,min:integer;
begin
for i:=1 to n do begin
lowcost[i]:=cost[v0,i];
closest[i]:=v0;
end;
for i:=1 to n-1 do begin
{尋找離生成樹最近的未加入頂點 k}
min:=maxlongint;
for j:=1 to n do
if (lowcost[j]<>0) then begin
min:=lowcost[j];
k:=j;
end;
lowcost[k]:=0; {將頂點k 加入生成樹}
{生成樹中增加一條新的邊 k 到 closest[k]}
{修正各點的 lowcost 和 closest 值}
for j:=1 to n do
if cost[k,j]
lowcost[j]:=cost[k,j];
closest[j]:=k;
end;
end;
end;

Kruskal演演算法

按權值遞增順序刪去圖中的邊，若不形成迴路則將此邊加入最小生成樹。
function find(v:integer):integer; {返回頂點 v 所在的集合}
var i:integer;
begin
i:=1;
while (i<=n) and (not v in vset) do inc(i);
if i<=n then find:=i else find:=0;
end;
procedure kruskal;
var
tot,i,j:integer;
begin
for i:=1 to n do vset:=i;{初始化定義 n 個集合，第 I個集合包含一個元素 I}
p:=n-1; q:=1; tot:=0; {p 為尚待加入的邊數，q 為邊集指針}
sort;
{對所有邊按權值遞增排序，存於 e中，e.v1 與 e.v2 為邊 I 所連接的兩個頂點的
序號，e.len 為第 I條邊的長度}
while p>0 do begin
i:=find(e[q].v1）;j:=find(e[q].v2）;
if i<>j then begin
inc(tot,e[q].len);
vset:=vset+vset[j];vset[j]:=[];
dec(p);
end;
inc(q);
end;
writeln(tot);
end;

C語言代碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
#include
#include
#include
#defineMAX_VERTEX_NUM20
#defineOK1
#defineERROR0
#defineMAX1000
typedefstructArcell
{
double adj ;
}Arcell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedefstruct
{
charvexs[MAX_VERTEX_NUM];//節點數組
AdjMatrixarcs;// 鄰接矩陣
intvexnum,arcnum;//圖的當前節點數和弧數
}MGraph;
typedefstructPnode//用於 普利姆 演演算法
{
charadjvex;//節點
doublelowcost;//權值
}Pnode,Closedge[MAX_VERTEX_NUM];//記錄頂點集U到V-U的代價最小的邊的輔助數組定義
typedefstructKnode//用於 克魯斯卡爾演演算法 中存儲一條邊及其對應的2個節點
{
charch1;//節點1
char ch2 ;//節點2
double value ;//權值
}Knode,Dgevalue[MAX_VERTEX_NUM];
//-------------------------------------------------------------------------------
intCreateUDG(MGraph&G,Dgevalue&dgevalue);
intLocateVex(MGraphG,charch);
intMinimum(MGraphG,Closedgeclosedge);
voidMiniSpanTree_PRIM(MGraphG,charu);
voidSortdge(Dgevalue&dgevalue,MGraphG);
//-------------------------------------------------------------------------------
intCreateUDG(MGraph&G,Dgevalue&dgevalue)//構造無向 加權圖 的鄰接矩陣
{
inti,j,k;
cout <<"請輸入圖中節點個數和邊/弧的條數：";
cin >>G.vexnum>>G.arcnum;
cout<<"請 輸入節點：";
for(i=0;i
cin>>G.vexs[i];
for(i=0;i
{
for(j=0;j
{
G.arcs[i][j].adj=MAX;
}
}
cout<<"請輸入一條邊依附的定點及邊的權值："<
for(k=0;k
{
cin>>dgevalue[k].ch1>>dgevalue[k].ch2>>dgevalue[k].value;
i=LocateVex(G,dgevalue[k].ch1）;
j=LocateVex(G,dgevalue[k].ch2）;
G.arcs[i][j].adj=dgevalue[k].value;
G.arcs[j][i].adj=G.arcs[i][j].adj;
}
returnOK;
}
intLocateVex(MGraphG,charch)//確定節點ch在圖G.vexs中的位置
{
inta;
for(inti=0;i
{
if(G.vexs[i]==ch)
a=i;
}
returna;
}
voidMiniSpanTree_PRIM(MGraphG,charu)//普利姆演演算法求最小 生成樹
{
inti,j,k;
Closedgeclosedge;
k=LocateVex(G,u);
for(j=0;j j++)
{
if(j!=k)
{
closedge[j].adjvex=u;
closedge[j].lowcost=G.arcs[k][j].adj;
}
}
closedge[k].lowcost=0;
for(i=1;i
{
k=Minimum(G,closedge);
cout<<"("<
closedge[k].lowcost=0;
for(j=0;j
{
if(G.arcs[k][j].adj
{
closedge[j].adjvex=G.vexs[k];
closedge[j].lowcost=G.arcs[k][j].adj;
}
}
}
}
intMinimum(MGraphG,Closedgeclosedge)//求closedge中權值最小的邊，並返回其頂點在vexs中的位置
{
inti,j;
doublek=1000;
for(i=0;i
{
if(closedge[i].lowcost!=0&&closedge[i].lowcost
{
k=closedge[i].lowcost;
j=i;
}
}
returnj;
}
voidMiniSpanTree_KRSL(MGraphG,Dgevalue&dgevalue)//克魯斯卡爾演演算法求最小生成樹
{
intp1, p2 ,i,j;
intbj[MAX_VERTEX_NUM];//標記數組
for(i=0;i
bj[i]=i;
Sortdge(dgevalue,G);//將所有權值按從小到大排序
for(i=0;i
{
p1=bj[LocateVex(G,dgevalue[i].ch1）];
p2=bj[LocateVex(G,dgevalue[i].ch2）];
if(p1!=p2）
{
cout<<"("<
for(j=0;j
{
if(bj[j]==p2）
bj[j]=p1;
}
}
}
}
voidSortdge(Dgevalue&dgevalue,MGraphG)//對dgevalue中各元素按權值按從小到大排序
{
inti,j;
double temp ;
charch1,ch2;
for(i=0;i
{
for(j=i;j
{
if(dgevalue[i].value>dgevalue[j].value)
{
temp=dgevalue[i].value;
dgevalue[i].value=dgevalue[j].value;
dgevalue[j].value=temp;
ch1=dgevalue[i].ch1;
dgevalue[i].ch1=dgevalue[j].ch1;
dgevalue[j].ch1=ch1;
ch2=dgevalue[i].ch2;
dgevalue[i].ch2=dgevalue[j].ch2;
dgevalue[j].ch2=ch2;
}
}
}
}
voidmain()
{
inti,j;
MGraphG;
charu;
Dgevaluedgevalue;
CreateUDG(G,dgevalue);
cout<<"圖的鄰接矩陣為："<
for(i=0;i
{
for(j=0;j
cout<
cout<
}
cout<<"=============普利姆演演算法===============\n";
cout<<"請輸入起始點：";
cin>>u;
cout<<"構成最小代價生成樹的邊集為：\n";
MiniSpanTree_PRIM(G,u);
cout<<"============ 克魯斯 科爾演演算法=============\n";
cout<<"構成最小代價生成樹的邊集為：\n";
MiniSpanTree_KRSL(G,dgevalue);
}

kruskal

program didi;
var
a:array[0..100000] of record
s,t,len:longint;
end;
fa,r:array[0..10000] of longint;
n,i,j,x,y,z:longint;
tot,ans:longint;
count,xx:longint;
procedure quick(l,r:longint);
var
i,j,x,y,t:longint;
begin
i:=l;j:=r;
x:=a[(l+r) div 2].len;
repeat
while x>a[i].len do inc(i);
while xdec(j);
if i<=j then
begin
y:=a[i].len;a[i].len:=a[j].len;a[j].len:=y;
y:=a[i].s;a[i].s:=a[j].s;a[j].s:=y;
y:=a[i].t;a[i].t:=a[j].t;a[j].t:=y;
inc(i);dec(j);
end;
until i>j;
if i
if l
end;
function find(x:longint):longint;
begin
if fa[x]<>x then fa[x]:=find(fa[x]);
find:=fa[x];
end;
procedure union(x,y:longint);{啟髮式合併}
var
t:longint;
begin
x:=find(x);
y:=find(y);
if r[x]>r[y] then
begin
t:=x;x:=y;y:=t;
end;
if r[x]=r[y] then inc(r[x]);
fa[x]:=y;
end;
begin
readln(xx,n);
for i:=1 to xx do fa[i]:=i;
for i:=1 to n do
begin
read(x,y,z);
inc(tot);
a[tot].s:=x;
a[tot].t:=y;
a[tot].len:=z;
end;
quick（1,tot);{將邊排序}
ans:=0;
count:=0;
i:=0;
while count<=x-1 do{count記錄加邊的總數}
begin
inc(i);
with a[i] do
if find(s)
begin
union(s,t);
ans:=ans+len;
inc(count);
end;
end;
write(ans);
end.

Prim

var
m,n:set of 1..100;
s,t,min,x,y,i,j,k,l,sum,p,ii:longint;
a:array[1..100,1..100]of longint;
begin
readln(p);
for ii:=1 to p do
begin
k:=0; sum:=0;
fillchar(a,sizeof(a),255);
readln(x);
m:=;
n:=[2..x];
for i:=1 to x do
begin
for j:=1 to x do
begin
read(a[i,j]);
if a[i,j]=0
then a[i,j]:=maxlongint;
end;
readln;
end;
for l:=1 to x-1 do
begin
min:=maxlongint;
for i:=1 to x do
if i in m
then begin
for j:=1 to x do
begin
if (a[i,j]
then begin
min:=a[i,j];
s:=i;
t:=j;
end;
end;
end;
sum:=sum+min;
m:=m+[t];
n:=n-[t];
inc(k);
end;
writeln(sum);
end;
end.
2張

基本信息

外文名
Minimum Spanning Tree,MST
應用學科
計算機，數學（圖論），數據結構
適用領域
應用圖論知識的實際問題
演算法
Kruskal演算法，Prim演算法