基本不等式
主要應用於求某些函數的最值及證明的不等式
基本不等式是主要應用於求某些函數的最值及證明的不等式。其表述為：兩個正實數的算術平均數大於或等於它們的幾何平均數。
在使用基本不等式時，要牢記“一正”“二定”“三相等”的七字真言。“一正”就是指兩個式子都為正數，“二定”是指應用基本不等式求最值時，和或積為定值，“三相等”是指當且僅當兩個式子相等時，才能取等號。
兩個正實數的算術平均數大於或等於它們的幾何平均數。
兩類最值問題
具體來說，利用基本不等式求最值包括下面兩種類型的題目：
已知x＞0；y＞0，則：
如果積xy是定值p，那麼當且僅當x=y時，x+y有最小值。(簡記：積定和最小)
如果和x+y是定值p，那麼當且僅當x=y時，xy有最大值。(簡記：和定積最大)
兩大技巧
“1”的妙用。題目中如果出現了兩個式子之和為常數，要求這兩個式子的倒數之和的最小值，通常用所求這個式子乘以1，然後把1用前面的常數表示出來，並將兩個式子展開即可計算。如果題目已知兩個式子倒數之和為常數，求兩個式子之和的最小值，方法同上。
調整係數。有時候求解兩個式子之積的最大值時，需要這兩個式子之和為常數，但是很多時候並不是常數，這時候需要對其中某些係數進行調整，以便使其和為常數。
公式
（a＞0，b＞0）
註：當且僅當a=b時取等
其中稱為的算術平均數，稱為 的幾何平均數。
變形
1、（當且僅當a=b 時取等號）
2、（a,b同號）
3、
4、
二元均值不等式
（調和均值≤幾何均值≤算術均值≤平方均值）當且僅當a=b時等號成立
常用不等式
∴a²+b²≥2ab
當 時，兩邊開平方
因為，所以當且僅當 時，不等式取等號。
在 中， ，點D 為 BC的中點，AE為高，設，
由射影定理，得
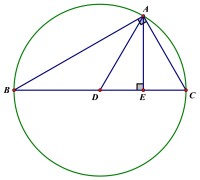
基本不等式的幾何證明
在 中，點D 為斜邊 BC的中點
中，
當且僅當AD 與AE 重合，即時等號成立
一般地，若 是正實數，則有均值不等式
當且僅當 時取等號
和定積最大
當 一定時， ，且當 時取等號
積定和最小
當 一定時， ，且當 時取等號
例：求 在 的最小值
解：由基本不等式可得，
當 即 時取等號
答：當 時，在 有最小值。
基本信息
- 中文名
- 基本不等式
- 外文名
- Inequality of arithmetic and geometric means AM–GM inequality
- 別名
- 二元均值不等式、算數 - 幾何平均值不等式
- 表達式
- a2+b2≥2ab
- 應用學科
- 數學
- 適用領域
- 不等式、理工科